Симметричной фигурой называется такая фигура, в которой отдельные части мысленно могут быть совмещены друг с другом посредством симметричного преобразования.
Симметричным преобразованием называется такое преобразование, при котором равные части фигуры совмещаются друг с другом.
Центр симметрии
Центр симметрии (С) – это точка внутри кристалла, по обе стороны от которой на равных расстояниях встречаются одинаковые точки кристалла. Симметричное преобразование, отвечающее центру симметрии, есть отражение в точке (зеркало – не плоскость, а точка). При таком отражении изображение поворачивается не только справа налево, но и с лица наизнанку.
Белым и синим изображены, соответственно, «лицевая» и «изнаночная» стороны фигуры.
Косой параллелепипед обладает центром симметрии С.
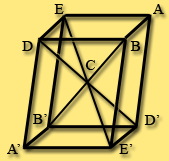
Для объемных кристаллов существует правило: центр симметрии в кристалле присутствует, если каждой грани кристалла соответствует грань равная и параллельная. Очень часто центр симметрии совпадает с центром тяжести кристалла.
Плоскость симметрии
Плоскость симметрии (Р) – это плоскость, которая делит кристалл на две зеркальные части, которые относятся друг к другу как предмет и его зеркальное отображение. Симметричное преобразование, отвечающее плоскости симметрии, есть отражение в плоскости.
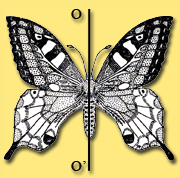
Симметрия бабочки характеризуется плоскостью симметрии ОО' (перпендикулярная к плоскости рисунка). Любое из двух крыльев как бы отражается в зеркале.
Трапеция и равнобедренный треугольник имеют плоскости симметрии, а параллелепипед – нет.
Ось симметрии
Ось симметрии (L) – это линия, при повороте вокруг которой на определенный угол кристалл совмещается сам с собой. Симметричное преобразование, отвечающее оси симметрии, есть поворот.
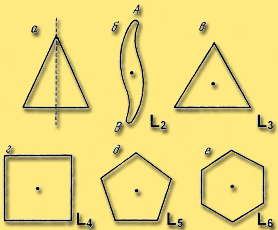
По углу поворота различают порядок оси симметрии. Минимальный угол поворота, при котором происходит совмещение фигуры, называется элементарным углом поворота оси.
Если элементарный угол поворота равен 180°, то порядок оси равен 
. Такая ось называется осью симметрии второго порядка. В треугольнике – ось симметрии 3 порядка; в квадрате – 4; в пятиугольнике – 5; в шестиугольнике – 6. На опыте установлено, что в кристаллах не может быть осей 5 порядка и порядка выше 6, т.е. 7, 8 …, хотя в живой природе они существуют: цветок лютика или морскую звезду характеризует ось 5 порядка, а осьминога – 8 порядка. Порядок оси симметрии ромашки или подсолнечника равен числу лепестков цветка. У круглого конуса или цилиндра есть ось симметрии бесконечного порядка, а у шара бесконечное число осей симметрии бесконечного порядка.
Каждому симметричному преобразованию соответствует некоторый геометрический образ. Эти геометрические образы называются элементами симметрии, с их помощью определяется симметрия кристаллов. Элементами симметрии являются: центр симметрии (С); плоскость симметрии (Р); ось симметрии (L).
Есть еще один элемент симметрии – трансляция – возможный только в бесконечных фигурах. Трансляция – это перенесение деталей структуры параллельно самим себе вдоль какого-либо направления.
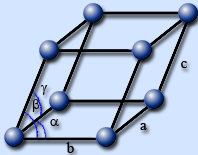
В кристаллической решетке можно выделить наименьший параллелепипед, перемещением которого во всех трех направлениях получается кристалл. Такая структурная единица называется элементарной ячейкой. Длины векторов трансляций а, b, c и углы между ними α, β, γ называются параметрами элементарной ячейки.
