Теорема 4.1. Пусть функции f₁, f₂,…, f_m: D → R, D `subset` Rⁿ, m ≤ n, f₁, f₂,…, f_m дифференцируемы в области D, rang 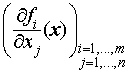 равен m для всех x`in` D. Тогда система функций {f₁, f₂,…, f_m} независима в D.



Доказательство этой теоремы почти очевидно: если бы система функций {f₁, f₂,…, f_m} была зависимой, то в матрице 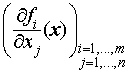 система строк была бы линейно зависимой. Тогда ранг этой матрицы уже не мог бы равняться m: он был бы меньше. Действительно, пусть f_m=φ(f₁,...,f_m-1). Тогда по правилу дифференцирования сложной функции имеем: , то есть последняя строка  матрицы 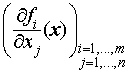 есть линейная комбинация предыдущих строк с коэффициентами 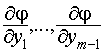, что и требовалось установить.