Пусть функция F(x,y,z) определена в некоторой области G пространства x, y, z. Рассмотрим уравнение

F(x,y,z) = 0.                  (1)

Может случиться, что каждой точке (x,y) из некоторой области A `sub` R² можно сопоставить такое значение z, что совокупность чисел x, y, z определяет точку из G и удовлетворяет уравнению (1). Обозначим полученную функциональную зависимость через

z = f (x,y), (x,y)`in` B.     (2)

По определению F(x,y, f (x,y)) = 0. Функция z = f (x,y), определяемая уравнением F(x,y, f (x,y)) = 0, называется неявной функцией.

Пример 2.1.

Пусть неявная функция определяется уравнением

x²+y²–z² = 0.                (3)

Разрешим это уравнение относительно z:

z = (x²+y²)^1/2,                (3.а)

z = –(x²+y²)^1/2.              (3.б)

Отсюда легко видеть, что каждой точке M(x,y) пространства переменных x, y, отличной от начала координат, соответствует два значения переменной z. Следовательно, нельзя задать однозначную функцию  z = f (x,y), определяемую уравнением (3), в области R³. Если же рассматривать уравнение (3) лишь в области {(x, y, z): z > 0}, то каждой точке M(x,y) двумерного пространства будет соответствовать лишь одно значение переменной z из рассматриваемого промежутка 0 < z < +∞. Это значение находится по формуле (3.а).

 

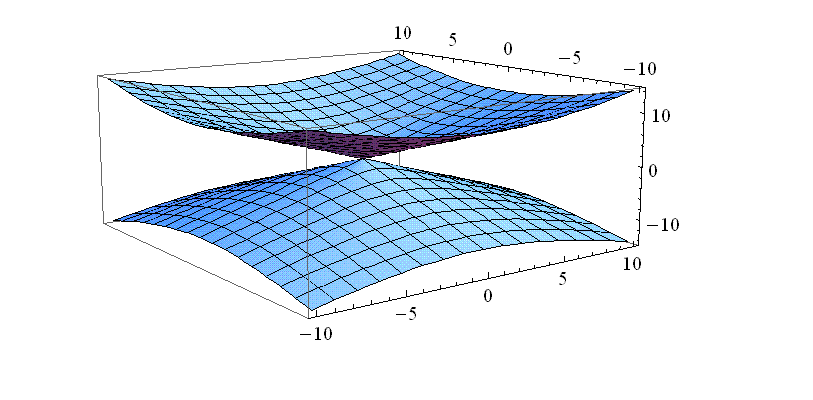
Графически множество { x²+y²–z² = 0 }, построенное в программе Mathematica, выглядит  так .

Из аналитической геометрии известно, что это – конус. И другие известные вам из курса аналитической геометрии уравнения поверхностей второго порядка можно рассматривать как неявные функции.