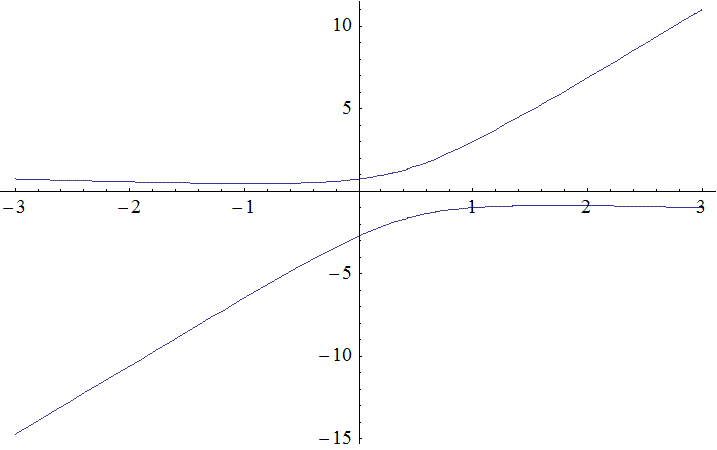Пусть в некоторой плоской области G задана функция F (x, y). Рассмотрим уравнение F(x, y) = 0. Может случиться так, что каждому значению переменной x из некоторого промежутка (x₀–a; x₀+a) соответствует такое значение переменной y, y = f(x), что F(x, f(x))=0. Такая функция y=f(x), определённая уравнением F(x, y) = 0, не разрешённым относительно y, называется неявной. Неявная функция может быть однозначной, когда каждому значению x соответствует только одно значение y, которое удовлетворяет уравнению F(x,y) = 0. Если же каждому значению x соответствует несколько значений y, удовлетворяющих уравнению F(x,y) = 0, неявная функция называется многозначной.

С неявными функциями вы уже наверняка встречались. Например, уравнение окружности x²+ y² = R² задаёт неявную функцию, которая принимает при каждом значении x, таком, что |x| < R, два различных значения (на верхней дуге окружности и на нижней дуге окружности). Таким образом, это многозначная неявная функция.  Также многозначными являются неявные функции, заданные каноническими уравнениями эллипса и гиперболы.

Другая возможность получить неявную функцию – это рассмотреть обратную функцию к функции y = f(x). Действительно: уравнение y – f(x) = 0 имеет вид F(x, y) = 0. Но в данном случае интересно ставить вопрос не о неявной функции y=f(x) (которая на самом деле является явной), а о функции x = g(y). Если такую однозначную функцию можно получить, то эта функция является обратной к y = f(x). В качестве примера можно рассмотреть функцию y = 2^x+x, которая строго возрастает на всей вещественной прямой. Эта функция является биекцией, значит, она имеет обратную, то есть существует однозначная неявная функция x = g(y), заданная уравнением y – 2^x+x = 0. Заметим, что эта функция g(y) не может быть выражена через элементарные функции. Такая ситуация возникает очень часто при работе с неявными функциями.

Пример 1.1. Рассмотрим уравнение

                                                              x²+ 4xy – y² – 2y + 2 = 0                                                      (1).

Функция x²+ 4xy – y²– 2y + 2 определена во всей плоскости переменных x, y. Разрешая уравнение (1) относительно y, получим:

                                                              y = 2x –1+(5x²– 4x + 3)^1⁄2,                                                   (1.а)

                                                              y = 2x – 1– (5x²– 4x + 3)^1⁄2 .                                                (1.б)

Здесь каждому значению x соответствуют два значения y, определяемые формулами (1.а) и (1.б). Следовательно, неявная функция, заданная уравнением (1), двузначна и распадается на две однозначные ветви (1.а) и (1.б).

Если сузить область определения функции x² + 4xy – y²– 2y + 2 , то можно добиться однозначности неявной функции. Легко видеть, что функция (1.а) принимает лишь положительные значения, а функция (1.б) − отрицательные. Поэтому, уравнение (1), рассматриваемое в верхней полуплоскости (y > 0), определяет y как однозначную функцию от x: y = 2x – 1+(5x² – 4x + 3)^1⁄2. Если же уравнение (1) рассматривать в нижней полуплоскости, то оно определит однозначную функцию (1.б).

 

Множество точек, заданное неявно уравнением x²+ 4xy – y²– 2y + 2 = 0, можно построить , используя программу Mathematica. Все наши выводы оказываются верными.