Неравенства вида

 

 

 

где  a, b, c  – действительные числа или выражения, зависящие от параметров, называются квадратными.

 

Решение квадратных неравенств основано на применении свойств квадратного трехчлена

 

,

 

которые допускают наглядную геометрическую интерпретацию.

 

Рассмотрим, например, неравенство

 

(1)

 

Возможны следующие случаи:

 

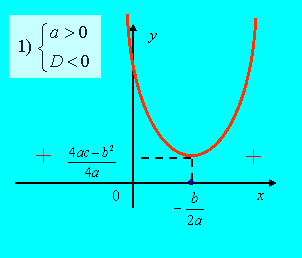
1)   Если   (рис. 28), то

 

.

 

2)   Если (рис. 29), то

 

.

 

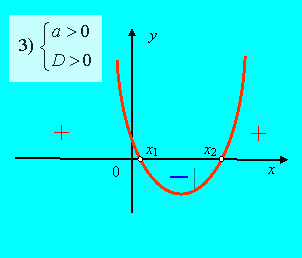
3)   Если   (рис. 30), то

 

,

 

где соответственно меньший и больший корень квадратного трехчлена.

 

4)   Если   (рис. 31), то

 

.

 

5)   Если  (рис. 32), то

 

.

 

6)   Если   (рис. 33), то

 

.

 

 

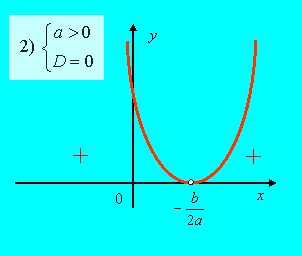Рис. 28	Рис. 29

 

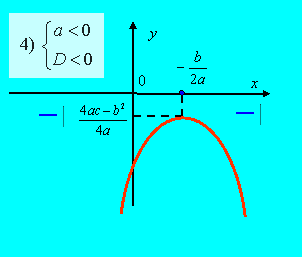Рис. 30	Рис. 31

 

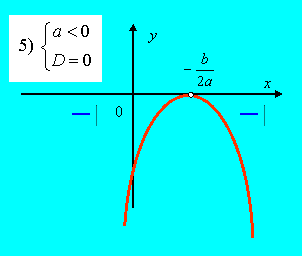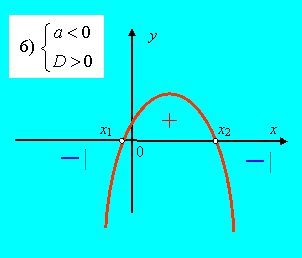Рис. 32	Рис. 33