1. Использование ОДЗ. Иногда ОДЗ уравнения состоит из нескольких точек, и остается только проверить, какие из них удовлетворяют уравнению. В случае, если ОДЗ – пустое множество, уравнение не имеет решений.
2. Разложение на множители (вынесение общего множителя). Если функция ![]() имеет вид
имеет вид ![]() , то уравнение
, то уравнение ![]() можно решать так:
можно решать так:
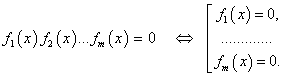 .
.
В конце необходимо сделать проверку.
3. Замена переменной. В тех случаях, когда исходное уравнение может быть приведено к виду ![]() , заменой
, заменой ![]() уравнение сводится к решению уравнения
уравнение сводится к решению уравнения ![]() . Далее для каждого полученного корня
. Далее для каждого полученного корня ![]() решается уравнение
решается уравнение ![]() .
.
4. Использование ограниченности функций. Иногда уравнение ![]() устроено так, что на ОДЗ
устроено так, что на ОДЗ ![]() , а
, а ![]() при некотором
при некотором ![]() . Решение уравнения сводится тогда к нахождению тех значений
. Решение уравнения сводится тогда к нахождению тех значений ![]() , для которых одновременно
, для которых одновременно ![]() и
и ![]() .
.
5. Использование монотонности функций. Если на некотором промежутке ![]() функции, входящие в уравнение
функции, входящие в уравнение ![]() , таковы, что
, таковы, что ![]() непрерывна и строго возрастает, а
непрерывна и строго возрастает, а ![]() непрерывна и строго убывает, то равенство
непрерывна и строго убывает, то равенство ![]() возможно только в одной точке. Иногда это значение можно угадать.
возможно только в одной точке. Иногда это значение можно угадать.
6. Графический метод. Иногда полезно рассмотреть эскизы графиков ![]() и
и ![]() , входящих в уравнение
, входящих в уравнение ![]() . Это может помочь выяснить: а) на какие множества надо разбить числовую ось, чтобы на каждом из этих множеств использовать свой способ решения; б) наличие или отсутствие корней, их количество.
. Это может помочь выяснить: а) на какие множества надо разбить числовую ось, чтобы на каждом из этих множеств использовать свой способ решения; б) наличие или отсутствие корней, их количество.