|
Тема. Решение задач по теме "Линзы. Построение изображений в тонкой линзе. Формула линзы". Цель:
Ход занятия Прежде чем приступить к выполнению задания, необходимо повторить определения главной и побочной оптических осей линзы, фокуса, фокальной плоскости, свойства основных лучей при построении изображений в тонких линзах, формулу тонкой линзы (собирающей и рассеивающей), определение оптической силы линзы, увеличения линзы. Для проведения занятия учащимся предлагается несколько расчетных задач с объяснением их решения и задачи для самостоятельной работы.
Качественные задачи
Примеры решения расчетных задач Задача 1. Заданы главная оптическая ось линзы NN, положение источника S и его изображения S´. Найдите построением положение оптического центра линзы С и ее фокусов для трех случаев (рис. 1). 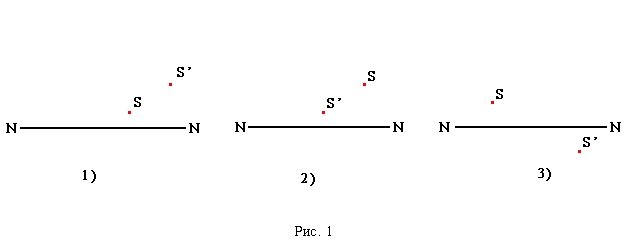 Решение: Для нахождения положения оптического центра С линзы и ее фокусов F используем основные свойства линзы и лучей, проходящих через оптический центр, фокусы линзы или параллельно главной оптической оси линзы. Случай 1. Предмет S и его изображение расположены по одну сторону от главной оптической оси NN (рис. 2).  Проведем через S и S´ прямую (побочную ось) до пересечения с главной оптической осью NN в точке С. Точка С определяет положение оптического центра линзы, расположенной перпендикулярно оси NN. Лучи, идущие через оптический центр С, не преломляются. Луч SA, параллельный NN, преломляется и идет через фокус F и изображение S´, причем через S´ идет продолжение луча SA. Это значит, что изображение S´ в линзе является мнимым. Предмет S расположен между оптическим центром и фокусом линзы. Линза является собирающей. Случай 2. Проведем через S и S´ побочную ось до пересечения с главной оптической осью NN в точке С - оптическом центре линзы (рис. 3).  Луч SA, параллельный NN, преломляясь, идет через фокус F и изображение S´, причем через S´ идет продолжение луча SA. Это значит, что изображение мнимое, а линза, как видно из построения, рассеивающая. Случай 3. Предмет S и его изображение лежат по разные стороны от главной оптической оси NN (рис. 4).  Соединив S и S´, находим положение оптического центра линзы и положение линзы. Луч SA, параллельный NN, преломляется и через фокус F идет в точку S´. Луч через оптический центр идет без преломления.
Задача 2. На рис. 5 изображен луч АВ, прошедший сквозь рассеивающую линзу. Постройте ход луча падающего, если положение фокусов линзы известно. 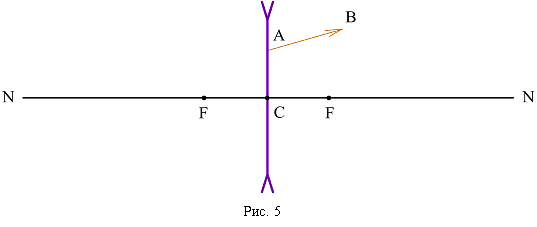 Решение: Продолжим луч АВ до пересечения с фокальной плоскостью РР в точке F´ и проведем побочную ось ОО через F´ и С (рис. 6). 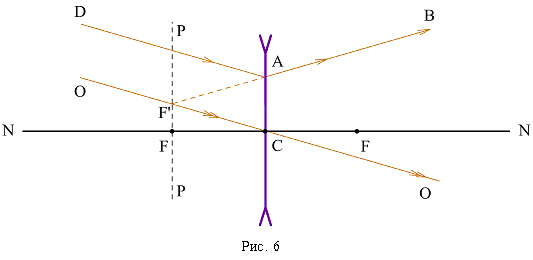 Луч, идущий вдоль побочной оси ОО, пройдет, не меняя своего направления, луч DA, параллельный ОО, преломляется по направлению АВ так, что его продолжение идет через точку F´. Задача 3. На собирающую линзу с фокусным расстоянием F1 = 40 см падает параллельный пучок лучей. Где следует поместить рассеивающую линзу с фокусным расстоянием F2 = 15 см, чтобы пучок лучей после прохождения двух линз остался параллельным? Решение:
По условию пучок падающих лучей ЕА параллелен главной оптической оси NN, после преломления в линзах он должен таковым и остаться. Это возможно, если рассеивающая линза расположена так, чтобы задние фокусы линз F1 и F2 совпали. Тогда продолжение луча АВ (рис. 7), падающего на рассеивающую линзу, проходит через ее фокус F2, и по правилу построения в рассеивающей линзе преломленный луч BD будет параллелен главной оптической оси NN, следовательно, параллелен лучу ЕА. Из рис. 7 видно, что рассеивающую линзу следует поместить на расстоянии d=F1-F2=(40-15)(см)=25 см от собирающей линзы.  Ответ: на расстоянии 25 см от собирающей линзы.
Задача 4. Высота пламени свечи 5 см. Линза дает на экране изображение этого пламени высотой 15 см. Не трогая линзы, свечу отодвинули на l = 1,5 см дальше от линзы и, придвинув экран, вновь получили резкое изображение пламени высотой 10 см. Определите главное фокусное расстояние F линзы и оптическую силу линзы в диоптриях. Решение:
Применим формулу тонкой линзы
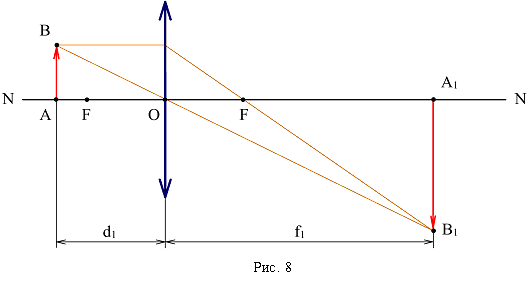 Из подобных треугольников АОВ и A1OB1 (рис. 8) поперечное увеличение линзы будет равно Аналогично для второго положения предмета после передвижения его на l:
Ответ: Задача 5. Двояковыпуклая линза, сделанная из стекла с показателем преломления n = 1,6, имеет фокусное расстояние F0 = 10 см в воздухе (n0 = 1). Чему будет равно фокусное расстояние F1 этой линзы, если ее поместить в прозрачную среду с показателем преломления n1 = 1,5? Определите фокусное расстояние F2 этой линзы в среде с показателем преломления n2 = 1,7. Решение: Оптическая сила тонкой линзы определяется формулой
Если линза находится в воздухе, то
Ответ: Задача 6. Система состоит из двух линз с одинаковыми по модулю фокусными расстояниями. Одна из линз собирающая, другая рассеивающая. Линзы расположены на одной оси на некотором расстоянии друг от друга. Известно, что если поменять линзы местами, то действительное изображение Луны, даваемое этой системой, сместится на l = 20 см. Найдите фокусное расстояние каждой из линз. Решение: Рассмотрим случай, когда параллельные лучи 1 и 2 падают на рассеивающую линзу (рис. 9). 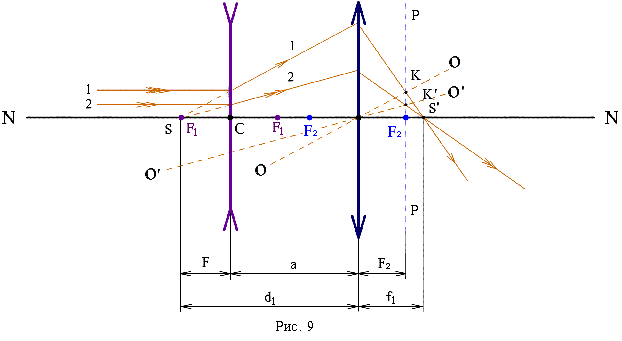 После преломления их продолжения пересекаются в точке S, являющейся фокусом рассеивающей линзы. Точка S является "предметом" для собирающей линзы. Ее изображение в собирающей линзе получим по правилам построения: лучи 1 и 2, падающие на собирающую линзу, после преломления проходят через точки пересечения соответствующих побочных оптических осей ОО и O´O´ с фокальной плоскостью РР собирающей линзы и пересекаются в точке S´ на главной оптической оси NN, на расстоянии f1 от собирающей линзы. Применим для собирающей линзы формулу
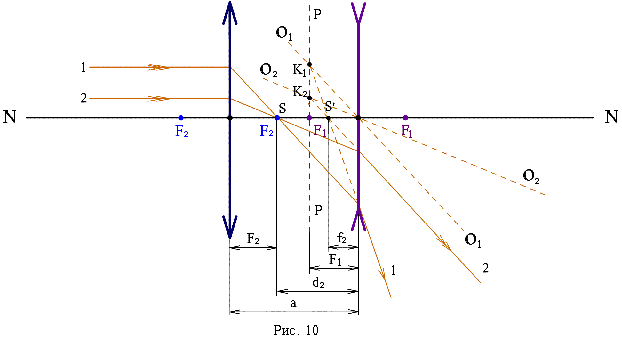 Пусть теперь лучи падают на собирающую линзу (рис. 10). Параллельные лучи 1 и 2 после преломления соберутся в точке S (фокусе собирающей линзы). Падая на рассеивающую линзу, лучи преломляются в рассеивающей линзе так, что продолжения этих лучей проходят через точки пересечения К1 и К2 соответствующих побочных осей О1О1 и О2О2 с фокальной плоскостью РР рассеивающей линзы. Изображение S´ находится в точке пересечения продолжений вышедших лучей 1 и 2 с главной оптической осью NN на расстоянии f2 от рассеивающей линзы.
l = f1 - (-f2) = Ответ: Задача 7. Собирающая линза дает на экране изображение S´ светящейся точки S, лежащей на главной оптической оси. Между линзой и экраном на расстоянии d = 20 см от экрана поместили рассеивающую линзу. Отодвигая экран от рассеивающей линзы, получили новое изображение S´´ светящейся точки S. При этом расстояние нового положения экрана от рассеивающей линзы равно f = 60 см. Определите фокусное расстояние F рассеивающей линзы и ее оптическую силу в диоптриях. Решение:  Изображение S´ (рис. 11) источника S в собирающей линзе Л1 находится на пересечении луча, идущего вдоль главной оптической оси NN и луча SA после преломления идущего в направлении AS´ по правилам построения (через точку К1 пересечения побочной оптической оси ОО, параллельной падающему лучу SA, с фокальной плоскостью Р1Р1 собирающей линзы). Если поставить рассеивающую линзу Л2, то луч AS´ изменяет направление в точке К, преломляясь (по правилу построения в рассеивающей линзе) в направлении KS´´. Продолжение KS´´ проходит через точку К2 пересечения побочной оптической оси 0´0´ с фокальной плоскостью Р2Р2 рассеивающей линзы Л2. По формуле для рассеивающей линзы
Отсюда Оптическая сила линзы Ответ: Задачи для самостоятельной работы
Рекомендуемая литература
|
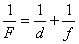 , где d - расстояние от предмета до линзы, f - расстояние от линзы до изображения, для двух положений предмета:
, где d - расстояние от предмета до линзы, f - расстояние от линзы до изображения, для двух положений предмета:
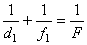 , (1)
, (1)
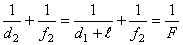 . (2)
. (2) =
= 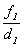 , откуда f1 = Γ1d1.
, откуда f1 = Γ1d1.
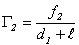 , откуда f2 = (d1 + l)Γ2.
, откуда f2 = (d1 + l)Γ2. . (3)
. (3)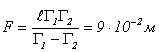 .
.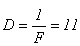 дптр.
дптр.
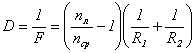 ,
,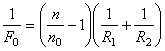 ; (4)
; (4)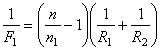 ; (5)
; (5)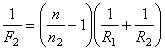 . (6)
. (6)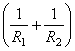 из (4):
из (4):
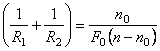 .
. см,
см,
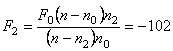 см.
см.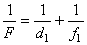 , (7)
, (7)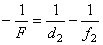 , (8)
, (8)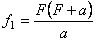 ,
, 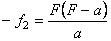 .
.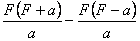 .
.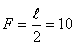 см.
см.
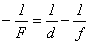 ,
,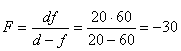 см.
см. дптр.
дптр.
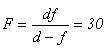 см,
см, 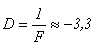 дптр.
дптр.
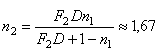 .
.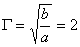 .
.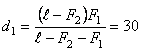 см перед первой линзой;
см перед первой линзой;
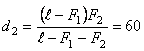 см за второй линзой.
см за второй линзой.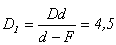 см.
см.