Тема. Решение задач по теме "Дифракция Френеля".

Цель:

- рассмотреть метод зон Френеля и основные приемы решения задач с применением метода зон Френеля.


Ход занятия

Прежде чем приступить к выполнению задания, необходимо повторить основные определения и понятия: явление дифракции, фронт волны, когерентные волны, принцип Гюйгенса-Френеля, условия максимума и минимума при дифракции Френеля.

Обратите внимание, что принципиальной разницы между интерференционной и дифракционной картинами нет.

Несколько задач предлагается с объяснением их решения. Задачи 5 и 6 не обязательны для всех учащихся, но интересующиеся смогут разобраться и оценить, насколько прост и нагляден метод зон Френеля для расчета интенсивности дифракционной картины с помощью спирали Френеля.


Качественные задачи
  1. Что такое зоны Френеля?
  2. Как объяснить периодические изменения освещенности на экране в центре дифракционной картины от круглого отверстия при монотонном изменении диаметра отверстия или расстояния от отверстия до экрана?

Примеры решения расчетных задач

Задача 1.

Точечный источник S монохроматического света с длиной волны λ=500нм на расстоянии а = 1 м от преграды, представляющей экран с круглым отверстием, диаметр которого d = 2 мм. Сколько зон Френеля укладывается в этом отверстии для точки наблюдения Р, находящейся на расстоянии b = 1 м от экрана? Постройте зоны Френеля для точки наблюдения Р.

Решение

От точечного источника S распространяется сферическая волна, волновая поверхность которой - сфера. Дойдя до экрана с отверстием, волны дифрагируют, то есть отклоняются от первоначального направления распространения. В соответствии с принципом Гюйгенса-Френеля каждая точка, до которой дошла волна, становится источником вторичных волн, распространяющихся во все стороны. Огибающая фронтов вторичных волн представляет новый фронт волны. Причем все вторичные волны когерентны, то есть могут в точке схождения интерферировать. Поэтому при определенных условиях в точке Р можно наблюдать интерференционную картину, получившуюся в результате дифракции волн. Чтобы объяснить наблюдаемую картину, проведем из точки Р конические поверхности до пересечения с волновой поверхностью DCD сферической волны (рис. 1). Длина PQ образующей конической поверхности равна 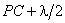, длина 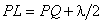, длина 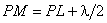и т.д. На волновой поверхности в результате построения образуются кольцевые зоны - зоны Френеля. Площади зон, как показывает расчет, приблизительно равны, однако действие этих зон в точке Р различно. Разность хода волн, приходящих в точку Р от любой зоны Френеля, не превышает 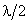(по построению). Поэтому в двух соседних зонах всегда есть такие соответствующие волны, разность хода между которыми в точке схождения Р равна 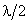. В точке Р эти волны встретятся в противофазе и погасят друг друга. Волны третьей зоны ослабят действие второй, а волны четвертой ослабят действие третьей и т.д. Если в отверстии DD укладывается только две зоны Френеля, то в точке Р почти не будет света, мы увидим темное пятно, окруженное светлым кольцом. Если в отверстии укладывается три зоны Френеля, то третья ослабит действие второй, свет от первой зоны пройдет, и в точке Р появится светлое пятно, окруженное темным кольцом, за которым вновь наблюдается светлое кольцо и т.д. Кольца становятся все тоньше по мере удаления от точки Р, а когда они сливаются, картина исчезает.



Таким образом, при четном числе зон Френеля в точке Р наблюдается темное пятно, окруженное чередующимися светлыми и темными кольцами, а при нечетном - светлое пятно, окруженное чередующимися темными и светлыми кольцами. Чем больше диаметр отверстия, тем больше зон Френеля укладывается в нем. В этом случае для нахождения суммарного действия всех зон в точке Р надо учитывать не только разности хода от двух соседних зон, но и плавное убывание амплитуды колебаний, приходящих в точку Р от более далеких, по сравнению с центральной, зон.

Получим выражение радиуса 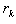зоны Френеля с номером k, отстоящей от источника S монохроматических волн длины λ на расстояние a, а от точки наблюдения P - на расстояние PD = b + 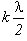. При этом a » λ, b » λ. Введем следующие обозначения (рис. 1):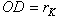, , 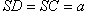PC=b, OC=x, PD = b + 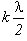. Из треугольников SOD и POD выразим 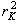по теореме Пифагора:



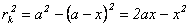
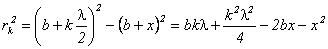
Приравняв правые части двух последних равенств, выразим х. Величиной 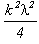можно пренебречь по сравнению с другими слагаемыми. Тогда получим:



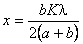
Подставим x в выражение для 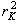. Тогда, пренебрегая вторым слагаемым, получим:



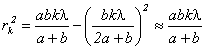
Отсюда внешний радиус 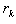k-той зоны Френеля будет равен


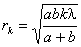         (1)

По условию задачи 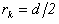. Выразим из (1) число зон k, укладывающихся в отверстии.



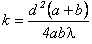
Подставляя численные значения, получим:



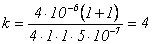
 Ответ: = 4, в точке Р будет темное пятно.



Задача 2.

Точечный источник монохроматического света длины волны λ=500нм находится на расстоянии а = 6,75 м от ширмы с круглым отверстием диаметра d = 4,5 мм. На расстоянии b = a от ширмы расположен экран (рис. 2). Как изменится освещенность в точке Р экрана, лежащей на оси пучка, если диаметр отверстия увеличить до значения d1 = 5,2 мм?



Решение

Для точки наблюдения Р из формулы (1) Задачи 1 выразим число зон Френеля и 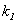, укладывающихся в отверстии ширмы диаметром соответственно d и d1.


;  .

;  .

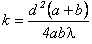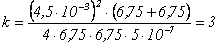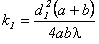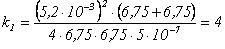Нечетному числу зон соответствует максимум освещенности, так как в этом случае колебания от третьей и второй зон Френеля, идущие в противофазе, ослабят друг друга, а свет от первой зоны пройдет полностью, в точке Р получим максимум освещенности.

При увеличении диаметра отверстия в точку Р придут волны от четырех зон Френеля. Они попарно ослабят друг друга, и в точке Р получим минимум освещенности.



Задача 3.

Как согласовать с законом сохранения энергии тот факт, что при увеличении диаметра отверстия ширмы (см. условие Задачи 2) освещенность на оси пучка может уменьшиться?


Решение

На самом деле при увеличении диаметра отверстия света проходит больше, суммарная освещенность экрана возрастает, но распределение световой энергии по экрану будет таково, что в центре будет темное пятно, окруженное чередующимися светлыми и темными кольцами.



Задача 4.

Плоская световая волна с длиной волны λ=600нм падает по нормали на экран с круглым отверстием. Определить диаметр отверстия, при котором в точке Р, лежащей на оси светового пучка на расстоянии b = 2 м от экрана, будет наблюдаться максимальная освещенность.

Решение

Максимальная освещенность в точке Р будет наблюдаться при условии, когда в отверстии уложится только первая зона Френеля. По условию падающая волна - плоская. Это значит, что фронт такой волны - плоскость, радиус кривизны а такой волны много больше b (а » b), учтем это в выражении для радиуса зоны Френеля:


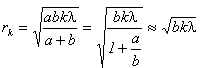(здесь учтено, что ).

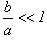Для k =1 имеем . Подставляя численные значения, получим:


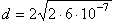м ≈ 2,2 мм.

 

Ответ:   ≈ 2,2 мм.



Задача 5.

На пути сферической световой волны находится преграда в виде непрозрачного круглого диска (рис. 3). Покажите, что в точке Р на оси светового пучка будет наблюдаться светлое пятно, если размеры диска достаточно малы.


Решение

Для расчета интенсивности света в точке наблюдения Р можно применить метод зон Френеля. Каждая зона имеет внутренний и внешний радиусы. При переходе от внутренней части зоны к внешней фаза волны изменяется на π, что соответствует разности хода 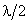. Если зону разбить на равные по площади кольцевые подзоны и действие каждой подзоны представить в виде вектора амплитуды 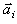, то сумма векторов 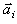всех подзон даст результирующий вектор амплитуды зоны Френеля. Он соединяет начало первого вектора 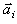и конец последнего. Из рис. 4 видно, что вектор 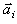в пределах каждой зоны поворачивается на π



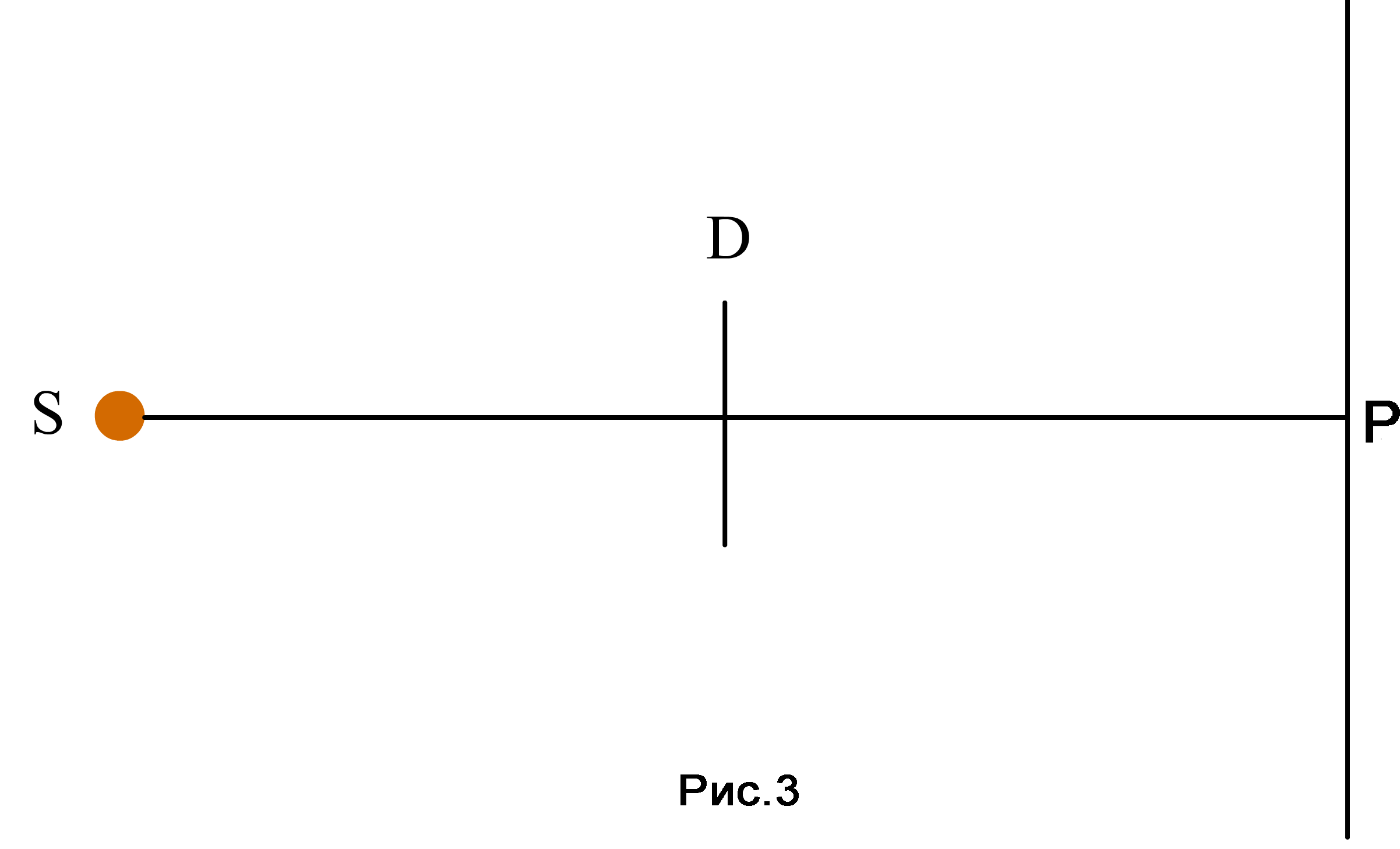
В пределе, когда число кольцевых зон будет неограниченно возрастать, а ширина стремиться к нулю, векторная диаграмма примет вид спирали (рис. 4д). Спираль Френеля позволяет оценить интенсивность освещенности в точке Р, так как интенсивность пропорциональна квадрату амплитуды. Из сравнения рис. 4а и 4д видно, что амплитуда при открытой первой зоне Френеля в два раза больше амплитуды А0 полностью открытого фронта, а интенсивность в точке P равна I1 = 4I0, то есть в четыре раза больше интенсивности при полностью открытом волновом фронте.



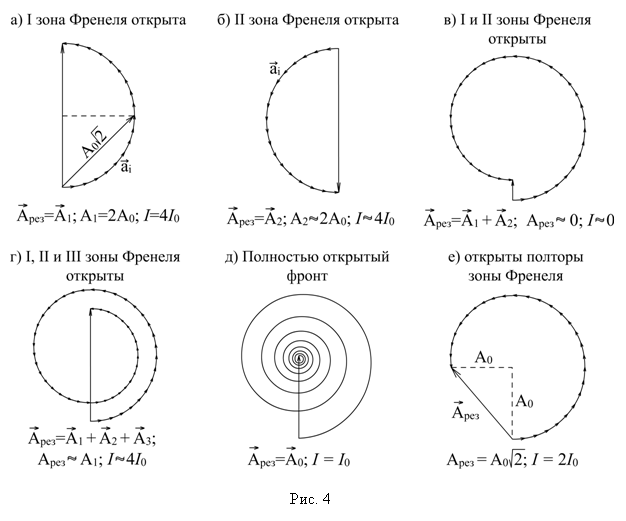
Если обозначить амплитуды колебаний от зон Френеля A1, A2, A3,..., то, учитывая направления векторов, описывающих колебания от различных зон Френеля, получим для результирующей амплитуды Aрез= A1 - A2 + A3 - A4 + A5 - ..., причем с ростом номера k зоны амплитуды уменьшаются. Учитывая это, результирующую амплитуду можно представить так:





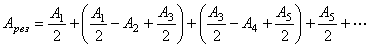
Выражения в скобках приблизительно равны нулю, поэтому




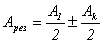
Если k - нечетное, нужно взять знак плюс, если четное - минус. Если число зон k велико, то 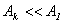, и мы получим результирующую амплитуду от полностью открытого фронта (рис. 4д):




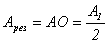
Полученный результат согласуется с рис. 4д.


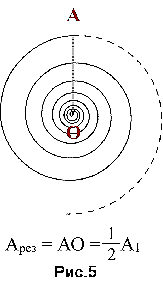
Если на пути сферического фронта волны находится преграда в виде диска, закрывающего для точки наблюдения Р первую зону Френеля, то пройдут волны от всех зон Френеля, начиная со второй. В точке Р амплитуда результирующего колебания будет



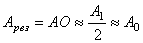
то есть амплитуда результирующего колебания равна половине амплитуды колебания, даваемого первой зоной (или амплитуде полностью открытого фронта).

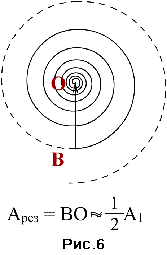
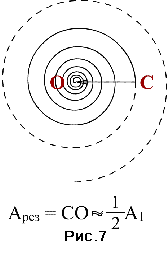
Если пройдут волны от зон, начиная с третьей, то 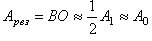(рис. 6). Если диск закроет 2,5 зоны, то 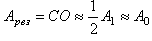(рис. 7), то есть в точке Р при достаточно малом размере диаметра диска будет всегда наблюдаться светлое пятно.



Задача 6.

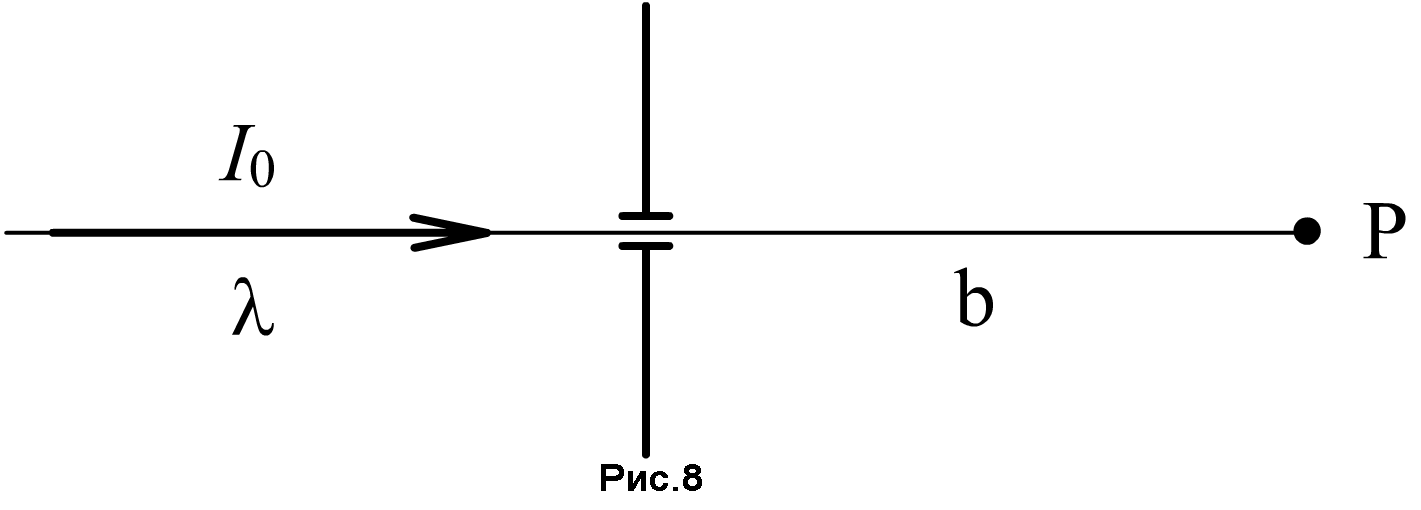
Плоская световая волна λ = 640нм с интенсивностью I0 падает нормально на непрозрачный экран с круглым отверстием, радиус которого γ = 1,2мм (рис. 8). Найдите интенсивность в центре дифракционной картины на экране, отстоящем на расстоянии b = 1,5 м от отверстия.



Решение

Плоская световая волна с интенсивностью I0 дифрагирует на отверстии, и в точке Р наблюдается интенсивность I, соответствующая числу зон Френеля, уложившихся в отверстии радиуса r, совпадающим с внешним радиусом 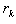k-той зоны Френеля.

Для плоской волны , , 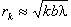отсюда найдем k - число зон Френеля, уложившихся в отверстии:



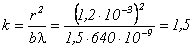
Значит, в точку Р приходят вторичные волны от 1,5 зоны Френеля (рис. 4е, Задача 5). Им соответствует колебание амплитуды Aрез. Этому колебанию соответствует вектор, соединяющий начало и конец спирали Френеля для 1,5 зон. Как видно из рис. 4а, , где A0 - амплитуда, соответствующая полностью открытому фронту (рис. 4д, Задача 5). Интенсивность пропорциональна квадрату амплитуды: , то есть интенсивность от 1,5 зон в два раза больше, чем от полностью открытого фронта.


Таким образом, с помощью спирали Френеля можно наглядно объяснить наблюдаемые чередования максимумов и минимумов дифракционной картины и оценить их интенсивность.


Задачи для самостоятельной работы
  1. Найдите радиусы первых трех зон Френеля:

    a) для сферической волны, если расстояние от источника света до волновой поверхности а = 1 м, расстояние от волновой поверхности до точки наблюдения b = 1 м. Длина волны λ = 500 нм;


    б) плоской волны, если расстояние от волновой поверхности до точки наблюдения b = 1 м. Длина волны λ = 500нм.

    Ответ: а) r1 = 0,5мм,r2 = 0,71 мм, r3 = 0,86 мм; б) r1 = 0,71 мм , r2 =1,0 мм , r3 = 1,22 мм.

  2. Дифракционная картина наблюдается на расстоянии l от точечного источника монохроматического света с длиной волны λ = 600нм. На расстоянии a = 0,5l от источника помещена круглая непрозрачная преграда диаметром D = 0,6 см. Найдите расстояние l, если преграда закрывает для точки наблюдения только центральную зону Френеля.

    Ответ: l = 60м.

  3. Точечный источник монохроматического излучения с длиной волны λ = 500нм находится на расстоянии l = 4 м от экрана. Посередине между источником и экраном помещена диафрагма с круглым отверстием. При каком радиусе R отверстия центр дифракционных колец, наблюдаемых на экране, будет наиболее темным?

    Ответ: R = 1мм.

  4. На диафрагму с диаметром отверстия D = 1,96 мм падает нормально параллельный пучок монохроматического света с длиной волны λ = 600нм. При каком наибольшем расстоянии L между диафрагмой и экраном в центре дифракционной картины на экране еще будет наблюдаться темное пятно?

    Ответ: L = 0,8м.

Рекомендуемая литература
  1. Касьянов В.А. Физика. 11 кл.: Учебн. для общеобразоват. учреждений. - 2-е изд., дополн. - М.: Дрофа, 2004. - С. 281-307.
  2. Элементарный учебник физики /Под ред акад. Г.С. Ландсберга. - Т. 3. - М.: Физматлит, 2000 и предшествующие издания.
  3. Бутиков Е.И., Кондратьев А.С. Физика. Т. 2. Электродинамика. Оптика. - М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. - С. 276-291.
  4. Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. - М.: Физматлит, 2005. - С. 247-251.
  5. Буховцев Б.Б., Кривченков В.Д., Мякишев Г.Я., Сараева И.М. Задачи по элементарной физике. - М.: Физматлит, 2000 и предшествующие издания.