Тема. Решение задач по теме «Свойства твердых тел »

 

Цели:

На примерах решения задач познакомить учащихся с основными типами задач и методами их решения.

 

Ход занятия

 Прежде всего, рассматриваются силы взаимодействия атомов в твердом теле. Выясняется связь между потенциальной энергией и силами взаимодействия атомов. Вводятся понятия линейного и объемного коэффициентов расширения. Обсуждается необходимость учета теплового расширения при решении задач строительства, транспорта и машиностроения.

1.       Почему атомы твердого тела находятся на вполне определенных расстояниях друг от друга?

2.       Как объяснить расширение тел при нагревании?

3.       Что такое коэффициент линейного расширения?

4.       Что такое коэффициент объемного расширения?

5.       Какова связь между коэффициентами линейного и объемного расширения?

 

Примеры решения задач

Задача 1. Под действием подвешенного груза медная проволока диаметром 4 мм получила такое же удлинение, как при нагревании на 20 °С. Найти вес груза. Для меди: a = 1,6×10^–6 К^–1; Е = 10×10¹⁰ Па.

Решение

Удлинение, получаемое проволокой под действием веса груза, равно ; удлинение, которое будет испытывать проволока при нагревании, равно . По условию , тогда ;

 Н.

Ответ: Р = 500 Н.

Задача 2. Железная линейка при 15 °С имеет длину 1 м. На сколько изменится длина линейки при охлаждении до –35 °С?     a = 1,2×10^–6 К^–1.

Решение

По закону линейного расширения

,                                                                                             (1)

,                                                                                            (2)

где  – длина линейки после ее охлаждения до температуры ; a – коэффициент расширения железа.

Тогда изменение длины линейки

.                     (3)

Найдя  из уравнения (1) и подставляя его в выражение (3), получаем

.                                                                                                  (4)

Учитывая, что , выражение (4) можно приближенно записать в виде

;

м.

Ответ: 6×10^–4 м.

 

Задача 3. Медная проволока, нагретая до температуры °С, натянута между двумя неподвижными стенками. При какой температуре, остывая, разорвется проволока (считать, что закон Гука справедлив вплоть до разрыва проволоки)? Предел прочности меди  Па. Модуль Юнга Е = 10×10¹⁰ Па,  К^–1.

 

Решение

Закон Гука для деформации растяжения:

,

где  – удлинение проволоки при нагревании;  – ее первоначальная длина; Е – модуль Юнга; s – напряжение.

Для разрыва проволоки необходимо, чтобы , где  – предел прочности. Таким образом,

.                                                                                                              (1)

При остывании длина проволоки изменяется по закону

,

где  – длина проволоки при °С.

Отсюда

;

.                                                                                                                (2)

Приравнивая правые части (1) и (2), получаем

;

С.

Температура, при которой разорвется проволока, равна

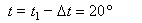С.

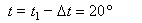Ответ: С.

 

Задача 4. На нагревание железного бруска израсходовано 1,68 МДж теплоты. Как изменился объем бруска?  К^-1.

Решение

По закону объемного расширения, , откуда

.

Здесь  – коэффициент объемного расширения железа, где a – коэффициент линейного расширения.

Количество теплоты, необходимое для нагревания бруска на DТ, равно

,

откуда . Поскольку масса бруска  , то

.

Изменение объема бруска

;  м³ » 1,69×10^–5 м³.

 

Ответ: м³.

 

Задания для самостоятельной работы

 

1. Часы с металлическим маятником спешат на  с  в сутки при температуре С и отстают на с  в сутки при температуре С. Найти температурный коэффициент  a  линейного расширения металла маятника, учитывая, что период колебаний маятника  (l – длина маятника, g – ускорение свободного падения).

Ответ:  К^–1.

Указание: найти отношение периодов при разных температурах.

 

2. Железный бак вмещает 50 л керосина при 0°С. Сколько керосина выльется из бака, если его внести в комнату с температурой 20 °С?

Плотность керосина при °С   кг/м³.

Коэффициент объемного расширения керосина  .

Коэффициент линейного расширения железа   К.

Ответ: кг.

 

3. Стальная балка закреплена между двумя стенами при температуре 10 °С. С какой силой концы балки будут давить на стены при температуре 35 °С?

Площадь поперечного сечения балки  см².

Модуль упругости стали ,

                                              К.

Ответ: .

 

4. При температуре °С   стеклянный баллон вмещает т = 100 г ртути. При °С  баллон вмещает т = 99,7 г   ртути. (В обоих случаях температуру ртути считать равной температуре баллона.) Найти температурный коэффициент линейного расширения стекла, учитывая, что температурный коэффициент объемного расширения ртути  К^–1.

Ответ:  К^–1,

где  – коэффициент объемного расширения стекла.

 

5. Какую длину должны иметь стальной и медный стержни при 0 °С, чтобы при любой температуре стальной стержень был длиннее медного на  см?

Коэффициенты линейного расширения стали    К^–1, меди -  К^–1.

Ответ:  см,

               см.