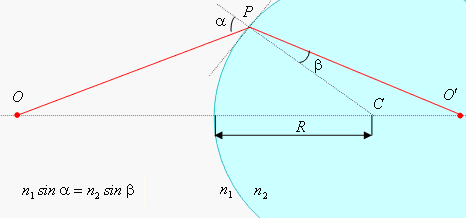
Преломление на сферической поверхности. Когда луч падает на сферическую границу раздела двух сред, построение отраженного и преломленного лучей производится следующим образом: строится плоскость касания в точке падения луча на сферическую поверхность и восстанавливается нормаль к этой плоскости в точке падения (рис. 6.25). Далее преломленный луч проводится в соответствии с законом преломления.

Рассмотрим преломление лучей на сферической поверхности прозрачной среды, такой, например, как одна из поверхностей линзы. Предположим, что источник света О находится в среде с показателем преломления 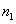, и лучи, исходящие из него, попадают в среду с показателем преломления  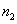(рис. 6.26). Пусть R – радиус кривизны сферической границы раздела этих сред, С – центр сферы. Покажем, что все лучи, выходящие из точки О, соберутся в одной точке 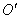, являющейся изображением точки О, если ограничиться лучами, составляющими малый угол с осью и друг с другом. Такие лучи называются параксиальными. Геометрическая оптика – наука неточная, и одно из важнейших ее упрощений – приближение параксиальной оптики. Суть его заключается в том, что рассматриваются только те лучи, которые на своем пути незначительно отклоняются от оптической оси системы. Тогда угол между оптической осью и падающим лучом настолько мал, что можно считать, что .

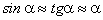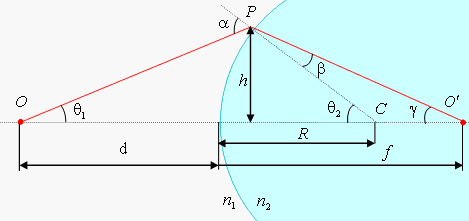
Рассмотрим один из лучей, выходящих из точки О. Луч преломится в точке Р на границе раздела двух сред, согласно закону преломления:

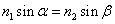Поскольку мы рассматриваем параксиальные лучи, то закон преломления можно записать следующим образом:

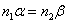Из рис. 6.26 видно, что 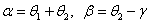, следовательно,

.

(6.3)

Вследствие малости углов 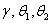 можно считать, что 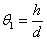, , 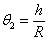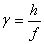. Подставляя значения углов в (6.3) и поделив все члены на h, получим

.

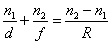(6.4)

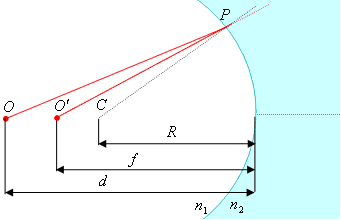Рис.6.27

Из (6.4) видно, что при заданном расстоянии d от сферической поверхности до источника расстояние от сферической поверхности до изображения f не зависит от угла, который луч образует с осью. Следовательно, все параксиальные лучи сходятся в одной точке .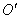

На рис. 6.26 лучи падают на выпуклую часть сферической поверхности. Но полученное соотношение (6.4) справедливо и для вогнутой поверхности. Это видно из рис. 6.27, если считать, что R и f являются отрицательными. Заметим, что в случае вогнутой поверхности изображение получается мнимым.