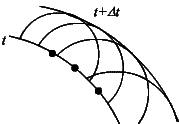
В XVIII столетии Христиан Гюйгенс на основе опытов с волнами на поверхности воды предложил метод построения волнового фронта. Если плоская волна падает на экран с отверстием, размер которого много меньше длины волны, то за экраном распространяется сферическая волна.

Рис. 3.5

На этом основании Гюйгенс предложил каждый элемент волнового фронта рассматривать как источник элементарных сферических волн – вторичных волн. Поскольку волновой фронт представляет совокупность точек среды, до которой дошла волна в момент времени t, то принцип Гюйгенса утверждает, что каждая точка среды, до которой доходит волновое движение, может рассматриваться как источник вторичных волн. Вторичные волны являются сферическими (рис. 3.5).

Во всех применениях вторичные волны Гюйгенса выступают не как реальные волны, а как вспомогательные сферы, используемые для такого построения. Эти сферы, построенные из точек волнового фронта как из центров, проявляют свое действие только на огибающей, которая дает новое положение волнового фронта. При этом остается необъясненным, почему при распространении волны не возникает обратная волна. Принцип Гюйгенса не дает никаких указаний об интенсивности волн, распространяющихся в различных направлениях. Этот недостаток был устранен Френелем.

Френель предположил, что вторичные волны когерентны и поэтому при наложении интерферируют друг с другом. Свет должен наблюдаться во всех местах пространства, где при интерференции вторичные волны усиливаются; где они взаимно гасят друг друга, должна наблюдаться темнота. К огибающей все вторичные волны приходят в одинаковых фазах, и их интерференция приводит к большой интенсивности света. Качественно становится понятным и отсутствие обратной волны. Вторичные волны, идущие назад, вступают в пространство, где уже есть волновое возмущение – прямая волна. При интерференции вторичные волны гасят прямую волну, так что после прохождения волны пространство за ней оказывается невозмущенным.

Расчет волнового поля в любой точке наблюдения Р на основе принципа Гюйгенса–Френеля делается следующим образом. Выделим поверхность S, все точки которой колеблются в одной фазе. Поверхность ограничивает объем с источниками света 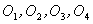 и т.д. (рис. 3.6). Все точки такой поверхности можно рассматривать как когерентные источники вторичных волн, распространяющихся во всех направлениях. Для того чтобы определить колебания в некоторой точке P, вызванные волной, нужно сначала определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от всех элементов поверхности S. Световое поле, возникающее в результате их интерференции, в пространстве вне поверхности S совпадает с полем реальных источников света.

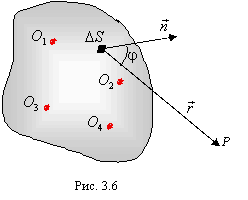Амплитуда вторичной волны пропорциональна площади элемента поверхности  и зависит от угла j между нормалью  к площадке  и направлением от площадки к точке наблюдения Р. Так как вторичные волны являются сферическими, то их амплитуда убывает с расстоянием по закону 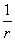, где 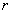 – расстояние от площадки  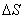до точки Р. От каждого участка  в точку наблюдения Р, лежащую перед поверхностью S, приходит колебание:

.

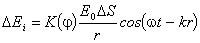(3.1)

Здесь  – фаза колебаний на поверхности ,  – волновое число,  – амплитуда светового колебания в том месте, где находится площадка . Коэффициент  зависит от угла . При  этот коэффициент максимален, при  – обращается в нуль.

Результирующее колебание в точке Р представляет собой суперпозицию колебаний (3.1), приходящих от всей волновой поверхности S:

.

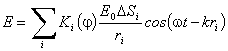(3.2)

Эта формула является аналитическим выражением принципа Гюйгенса–Френеля. Для качественного рассмотрения простейших случаев дифракции света с помощью принципа Гюйгенса–Френеля может быть применено построение зон Френеля.