Рассмотрим идеализированный случай сложения двух монохроматических волн одинаковой частоты. Уравнение плоской монохроматической волны, распространяющейся в положительном направлении оси X, имеет вид:

Если амплитуда и начальная фаза одинаковы во все моменты времени во всем пространстве, то волна называется однородной. Строго монохроматические волны никогда не могут быть точно реализованы в действительности и представляют идеализацию реальных волновых процессов. Условия применимости этой идеализации в каждой конкретной задаче требуют специального рассмотрения.

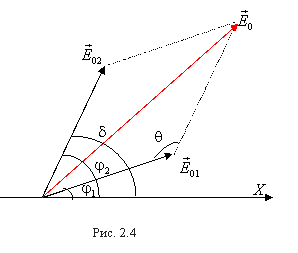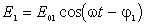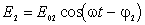Пусть две плоские монохроматические волны одной частоты, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления: и , где , .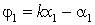

Для сложения колебаний воспользуемся методом векторной диаграммы. Как видно из рис. 2.4, согласно теореме косинусов амплитуда результирующего колебания будет равна

Так как угол , то амплитуда результирующего колебания в данной точке определится выражением: , а интенсивность:

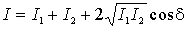(2.4)

где .

Если , , то интенсивность максимальна: , если , то интенсивность минимальна: .

Таким образом, при наложении двух монохроматических волн происходит устойчивое во времени перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности. В тех точках пространства, для которых , результирующая интенсивность ; в точках, где , результирующая интенсивность .

Особенно отчетливо проявляется интерференция в том случае, когда интенсивности обеих интерферирующих волн одинаковы: 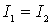. Тогда в максимумах 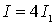, в минимумах же 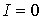. Для некогерентных волн при том же условии получается всюду одинаковая интенсивность .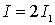