Из рис. 2.2 и 2.3 следует, что формулы, выражающие соответствующие законы, упростятся,
если перенести начало координат в точку с температурой –273º С. Для этого введем новую
шкалу температур и будем обозначать новую температуру Т, величину градуса оставим
той же, что и в шкале Цельсия. Тогда
отсюда
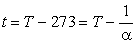 . . |
|
Запишем закон Шарля:
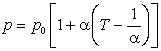 , ,
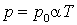 . .
|
(2.1) |
Аналогично для закона Гей-Люссака:
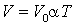 . . |
(2.2) |
Температура, введенная таким образом, называется абсолютной, а соответствующая температурная шкала – шкалой Кельвина, предложившего ее в 1848 г.
Из (2.1) и (2.2) при Т = 0 получается р = 0 и V = 0, чего,
конечно, быть не может. Это неожиданное следствие получилось в результате применения
рассмотренных законов для очень низких температур. Конечно, всякий реальный газ
превратится в жидкость и затвердеет, прежде чем будет достигнута температура
t = –273º C. Всякий физический закон имеет свои пределы применения.
Чтобы получить уравнение состояния идеального газа, рассмотрим некоторую массу газа m,
которая занимает объем V1, имеет давление P1 и находится при температуре T1.
Пусть эта же масса газа в другом состоянии имеет объем V2, давление P2 и температуру T2.
Перевести этот газ в другое состояние легко, если он находится в цилиндре под поршнем.
Сначала, не меняя давление P1, нагреем газ до температуры T2,
тогда он займет объем V' и этот объем по формуле (2.2) будет
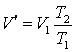 . . |
(2.3) |
Для того чтобы перевести его в окончательное состояние
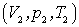
,
проведем изотермическое изменение объема, для которого
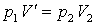 . . |
|
Теперь подставим значение объема
V' из (2.3):
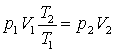 . . |
|
или
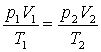 . . |
|
Полученное для данной массы
m соотношение указывает, что для любых двух состояний
величина
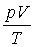
остается неизменной.
Обозначим это так:
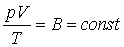 . . |
(2.4) |
Это соотношение было получено французским инженером Клапейроном в 1834 г. Конечно, для другой массы газа постоянная величина В имеет другое значение.
Менделеев преобразовал уравнение Клапейрона, использовав закон Авогадро. Согласно этому закону при одинаковых давлениях и температурах объемы одного моля всех газов одинаковы. Таким образом, если
то
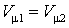 , , |
|
где
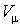
– объем одного моля газа.
В частности, при нормальных условиях,
т.е. при 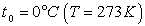 и
и 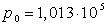 Па объем одного моля
любого газа равен
Па объем одного моля
любого газа равен 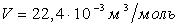 .
.
Если соотношение (2.4) относить к одному молю, то постоянная В будет одинакова для
любого газа. Обозначая ее через R, получим:
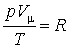 . . |
|
Однако теперь в этой формуле
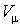
– объем одного моля.
Итак,
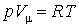 . . |
|
Это и есть уравнение состояния для определенной массы, именно для одного моля.
В такой форме оно было получено Менделеевым в 1875 г. и называется уравнением Клапейрона-Менделеева. Постоянная R называется универсальной газовой постоянной и является одной из основных физических констант.
Вычислим ее значение. Для этого рассмотрим 1 моль газа при нормальных условиях.
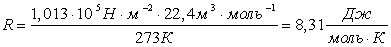 . . |
|
Обобщим уравнение Клапейрона-Менделеева для произвольной массы идеального газа.
Пусть газ с молярной массой μ взят в произвольном количестве, т.е. его масса m,
а объем равен V. Величина 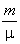 определяет,
сколько молей содержится в массе m. Объем одного моля
определяет,
сколько молей содержится в массе m. Объем одного моля 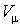 ,
тогда объем массы m:
,
тогда объем массы m:
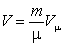 . . |
|
Отсюда следует, что для массы
m
выражение
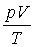
будет
в
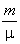
раз больше газовой постоянной
R.
Но
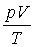
остается постоянным при всех изменениях газа, следовательно, для массы
m:
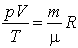 . . |
|
или
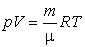 . . |
|
Эта формула связывает все четыре величины и употребляется во всех случаях, когда приходится иметь дело с газами.
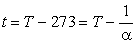 .
.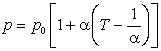 ,
,
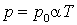 .
.
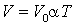 .
.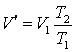 .
.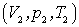 ,
проведем изотермическое изменение объема, для которого
,
проведем изотермическое изменение объема, для которого
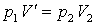 .
.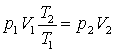 .
.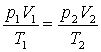 .
.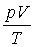 остается неизменной.
остается неизменной.
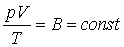 .
.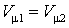 ,
,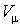 – объем одного моля газа.
– объем одного моля газа.
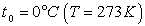 и
и 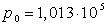 Па объем одного моля
любого газа равен
Па объем одного моля
любого газа равен 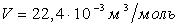 .
.
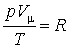 .
.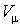 – объем одного моля.
– объем одного моля.
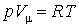 .
.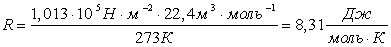 .
.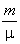 определяет,
сколько молей содержится в массе m. Объем одного моля
определяет,
сколько молей содержится в массе m. Объем одного моля 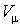 ,
тогда объем массы m:
,
тогда объем массы m:
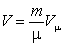 .
.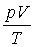 будет
в
будет
в 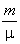 раз больше газовой постоянной R.
Но
раз больше газовой постоянной R.
Но 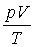 остается постоянным при всех изменениях газа, следовательно, для массы m:
остается постоянным при всех изменениях газа, следовательно, для массы m:
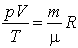 .
.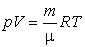 .
.