Явления, которые возникают на границе двух несмешивающихся жидкостей, определяются силами поверхностного натяжения. Хорошо известно, что разные жидкости ведут себя по-разному. Так, капля масла, помещенная на поверхность воды, принимает форму линзы, а капля бензина растекается на поверхности воды, образуя очень тонкую пленку.
Рассмотрим условия, при которых реализуется та или другая ситуация. Пусть имеем границу трех сред: жидкость 1 граничит с жидкостью 2, жидкости 1 и 2 граничат со средой 3, которая представляет собой смесь воздуха и паров жидкостей 1 и 2.
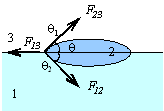
Рис. 6.21 |
Рассмотрим случай, когда капля жидкости 2 под действием силы тяжести втягивается в
жидкость 1, приобретая форму линзы (рис. 6.21). Граница соприкосновения трех сред
представляет собой окружность. На каждый элемент длины Δl этой окружности действуют
три силы:
Все эти силы направлены по касательным к поверхностям соприкосновения граничащих
сред,
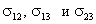
– коэффициенты поверхностного натяжения на соответствующих границах раздела.
Поскольку газовые среды оказывают слабое влияние на поверхностное натяжение граничащей с
ними жидкости, то можно приблизительно считать, что 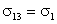 и
и 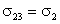 .
Капля жидкости 2 будет находиться в равновесии при условии, что все действующие на нее силы
друг друга взаимно уравновешивают. Спроектировав все действующие на каплю 2 силы на
горизонтальное и вертикальное направления, получаем
.
Капля жидкости 2 будет находиться в равновесии при условии, что все действующие на нее силы
друг друга взаимно уравновешивают. Спроектировав все действующие на каплю 2 силы на
горизонтальное и вертикальное направления, получаем
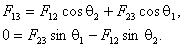 |
(6.30) |
Используя выражения (6.29), равенства (6.30) можно представить в виде:
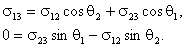 |
(6.31) |
Возведя в квадрат последние соотношения и сложив их, получаем:
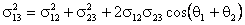 |
(6.32) |
Используя обозначение
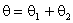
, равенство (6.32) можно записать в виде:
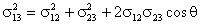 |
(6.33) |
Полученное равенство показывает, что угол θ определяется значениями коэффициентов поверхностного натяжения, то есть, в конечном счете, силами молекулярного взаимодействия между молекулами каждой жидкости и молекулами граничащих с ней сред.
Очевидно, что при некотором соотношении между 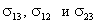 может возникнуть ситуация, при которой cosθ окажется равным единице. Это означает, что
угол θ равен нулю. Значение краевого угла θ = 0 соответствует условию, при котором
жидкость 2 растекается по поверхности жидкости 1 в виде очень тонкой пленки. В этом случае
принято говорить, что жидкость 2 полностью смачивает жидкость 1. Таким образом, полное
смачивание наблюдается при выполнении условия
может возникнуть ситуация, при которой cosθ окажется равным единице. Это означает, что
угол θ равен нулю. Значение краевого угла θ = 0 соответствует условию, при котором
жидкость 2 растекается по поверхности жидкости 1 в виде очень тонкой пленки. В этом случае
принято говорить, что жидкость 2 полностью смачивает жидкость 1. Таким образом, полное
смачивание наблюдается при выполнении условия
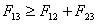 |
(6.34) |
В том случае, когда выполняется неравенство
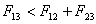 |
(6.35) |
капля жидкости 2 на поверхности жидкости 1 будет стягиваться до тех пор, пока не наступит ситуация, соответствующая выполнению условия
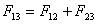 |
(6.36) |
Это условие определяет положение жидкости 2 на поверхности жидкости 1 в виде двояковыпуклой линзы, как это представлено на рис. 6.21.
Рассмотрим условия смачивания и несмачивания на границе жидкости с твердым телом. Следует отметить, что поверхностным натяжением обладают не только жидкости, но и твердые тела. Наличие в твердых телах строго периодической кристаллической структуры свидетельствует о наличии в них сил притяжения между молекулами. Благодаря наличию этих сил поверхностное натяжение возникает и в твердых телах.

Рис. 6.22 |
Пусть капля жидкости 2 помещена на поверхность твердого тела 1 (рис. 6.22). На рисунке
указаны силы поверхностного натяжения, действующие на границе жидкость-твердое
тело (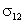 ), жидкость-газ (
), жидкость-газ (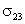 ) и твердое тело-газ (
) и твердое тело-газ (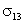 ).
Ясно, что поведение капли на поверхности твердого тела зависит от величины этих сил.
).
Ясно, что поведение капли на поверхности твердого тела зависит от величины этих сил.
Рассмотрим два случая. Если
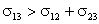 , , |
(6.37) |
то жидкость 2 растекается по поверхности тела 1 до образования очень тонкой пленки вплоть
до образования мономолекулярного слоя. При выполнении этого условия наступает полное
смачивание жидкостью поверхности твердого тела. Угол θ при этом равен 0. Если при
некотором соотношении между
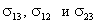
, а также
значении
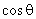
оказывается справедливым равенство
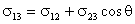 , , |
(6.38) |
то имеет место так называемое неполное смачивание. Жидкость 2 растекается по поверхности твердого тела до тех пор, пока не выполнится равенство (6.38).
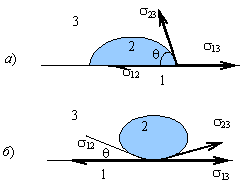
Рис. 6.23 |
Угол θ при этом является острым (рис. 6.23а). Некоторые жидкости на поверхности твердого
тела образуют капли, равновесная форма которых определяется неравенством
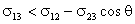 . . |
(6.39) |
При этом угол θ является тупым углом (рис. 6.23б).
Силы
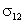
и
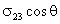
стремятся придать капле сферическую форму, чему препятствует действующая на каплю сила тяжести. В этом случае имеет место частичное несмачивание.
В реальной ситуации при взаимодействии жидкости с твердым телом реализуются, как правило,
две возможности – либо частичное смачивание 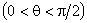 ,
либо частичное несмачивание
,
либо частичное несмачивание 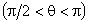 .
.
Это интересно

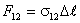 ,
,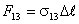 ,
,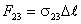 .
.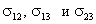 – коэффициенты поверхностного натяжения на соответствующих границах раздела.
– коэффициенты поверхностного натяжения на соответствующих границах раздела.
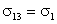 и
и 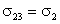 .
Капля жидкости 2 будет находиться в равновесии при условии, что все действующие на нее силы
друг друга взаимно уравновешивают. Спроектировав все действующие на каплю 2 силы на
горизонтальное и вертикальное направления, получаем
.
Капля жидкости 2 будет находиться в равновесии при условии, что все действующие на нее силы
друг друга взаимно уравновешивают. Спроектировав все действующие на каплю 2 силы на
горизонтальное и вертикальное направления, получаем
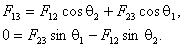
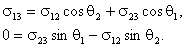
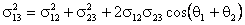
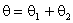 , равенство (6.32) можно записать в виде:
, равенство (6.32) можно записать в виде:
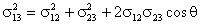
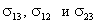 может возникнуть ситуация, при которой cosθ окажется равным единице. Это означает, что
угол θ равен нулю. Значение краевого угла θ = 0 соответствует условию, при котором
жидкость 2 растекается по поверхности жидкости 1 в виде очень тонкой пленки. В этом случае
принято говорить, что жидкость 2 полностью смачивает жидкость 1. Таким образом, полное
смачивание наблюдается при выполнении условия
может возникнуть ситуация, при которой cosθ окажется равным единице. Это означает, что
угол θ равен нулю. Значение краевого угла θ = 0 соответствует условию, при котором
жидкость 2 растекается по поверхности жидкости 1 в виде очень тонкой пленки. В этом случае
принято говорить, что жидкость 2 полностью смачивает жидкость 1. Таким образом, полное
смачивание наблюдается при выполнении условия
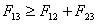
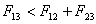
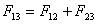

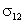 ), жидкость-газ (
), жидкость-газ (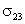 ) и твердое тело-газ (
) и твердое тело-газ (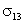 ).
Ясно, что поведение капли на поверхности твердого тела зависит от величины этих сил.
).
Ясно, что поведение капли на поверхности твердого тела зависит от величины этих сил.
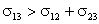 ,
,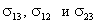 , а также
значении
, а также
значении 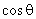 оказывается справедливым равенство
оказывается справедливым равенство
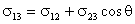 ,
,
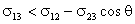 .
.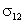 и
и 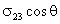 стремятся придать капле сферическую форму, чему препятствует действующая на каплю сила тяжести. В этом случае имеет место частичное несмачивание.
стремятся придать капле сферическую форму, чему препятствует действующая на каплю сила тяжести. В этом случае имеет место частичное несмачивание.
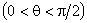 ,
либо частичное несмачивание
,
либо частичное несмачивание 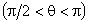 .
.