В жизни часто приходится иметь дело с телами, пронизанными множеством мелких каналов (бумага, пряжа, кожа, почва, дерево). Приходя в соприкосновение с водой или другими жидкостями, такие тела очень часто впитывают в себя жидкость. На этом основано действие полотенца, фитиля в лампе, питание растений. Подобные явления можно также наблюдать в очень узких стеклянных трубочках, которые называются капиллярными (от латинского слова "капилля" – волос).

Для капиллярных сосудов характерна прежде всего кривизна поверхности жидкости в них, поэтому в таких сосудах в полной мере проявляются эффекты, обусловленные избыточным давлением Лапласа. К числу таких эффектов относится капиллярный подъем.

Рис. 6.17

Найдем высоту поднятия жидкости в цилиндрической капиллярной трубочке радиуса r (рис. 6.17а). Пусть жидкость смачивает поверхность трубочки, вследствие чего в последней образуется симметричный вогнутый мениск с радиусами кривизны двух взаимно перпендикулярных сечений 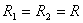. Отметим еще, что изменением давления жидкости при ее поднятии на высоту порядка r будем пренебрегать. В этом приближении давление во всех точках мениска можно считать одинаковым.

Под искривленной поверхностью вогнутого мениска давление в жидкости, как это было рассмотрено выше, меньше атмосферного давления Р₀ на величину давления Лапласа 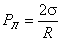(рис. 6.17б).

Под действием возникшей разности давлений на уровне поверхности жидкости в широком сосуде и непосредственно под мениском в капиллярной трубочке жидкость начинает подниматься по трубочке, и будет подниматься до тех пор, пока гидростатическое давление поднявшегося столба жидкости не будет равно давлению Лапласа.

Условие равновесия жидкости в капиллярной трубочке определяется равенством

.

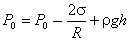(6.23)

Из (6.23) следует:

.

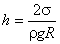(6.24)

Из рис. 6.18 следует, что

.

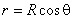(6.25)

Подставляя (6.25) в (6.24), получаем:

.

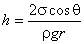(6.26)

Рис. 6.18

Полученная формула, определяющая высоту поднятия жидкости в капиллярной трубочке, носит название формулы Жюрена. Очевидно, что чем меньше радиус трубки, тем на большую высоту поднимается в ней жидкость. Кроме того, высота поднятия растет с увеличением коэффициента поверхностного натяжения жидкости.

В частном случае для жидкости, полностью смачивающей стенки капилляра 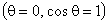, формула Жюрена принимает вид:

.

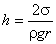(6.27)

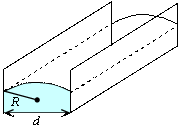
Рис. 6.19

Капиллярный подъем может наблюдаться не только в цилиндрических капиллярах. Жидкость поднимается и между двумя пластинами, разделенными узким зазором (рис. 6.19). Если пластины параллельны друг другу, то мениск имеет цилиндрическую форму с радиусом кривизны одного из сечений, равным 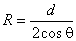. Радиус кривизны другого нормального сечения цилиндрического мениска можно считать равным бесконечности. При этом условии высота поднятия жидкости между пластинами равна:

.

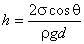(6.28)

В формуле учтено, что давление Лапласа при цилиндрическом мениске равно .

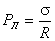Если жидкость не смачивает капилляр, то в трубочке образуется выпуклый мениск, центр кривизны которого не вне, а внутри жидкости. В этом случае добавочное давление Лапласа направлено вниз. Уровень жидкости в капиллярной трубочке опускается ниже уровня жидкости в широкой части сосуда. Говорят, что имеет место отрицательный капиллярный подъем (рис. 6.20). Отметим еще, что формула Жюрена может быть использована для экспериментального определения коэффициента поверхностного натяжения жидкости. Для этого нужно измерить радиус капиллярной трубочки и высоту поднятия в ней жидкости.

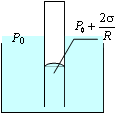
Рис. 6.20

В заключение подчеркнем, что явления, обусловленные капиллярностью, играют большую роль в природе, особенно велико их значение в живых организмах, значительная часть кровеносной системы которых представляет собой мельчайшие капилляры.