Из первого начала термодинамики вытекает существование у каждой системы некоторой функции состояния – внутренней энергии, которая обладает двумя важными свойствами:
1. Изменение этой функции не зависит от пути перехода системы из одного состояния в другое, а зависит лишь от начального и конечного состояний.
2. Если система совершает равновесный круговой процесс, то изменение ее внутренней энергии в этом процессе равно нулю.
Покажем, что из второго начала термодинамики вытекает существование другой функции состояния, обладающей этими свойствами.
Как следует из соотношения (4.42), для обратимого цикла Карно справедливо равенство
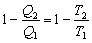 , , |
(4.43) |
 . . |
(4.44) |

Рис. 4.17 |
Отношение количества теплоты, полученного системой в изотермическом процессе, к температуре этого процесса называется приведенной теплотой. Следовательно, из соотношения (4.44) видно, что приведенная теплота при переходе системы из состояния 1 в состояние 3 по пути 1→2→3 (рис. 4.17) равна приведенной теплоте при переходе системы из состояния 1 в состояние 3 по пути 1→4→3. Это дает возможность утверждать, что система обладает некоторым физическим свойством, которое может быть представлено как функция ее состояния, поскольку это свойство системы не зависит от пути, по которому система перешла из начального состояния в конечное. Это свойство принято называть энтропией.
Идея назвать новую функцию состояния энтропией принадлежит Клаузиусу. Он так объяснил смысл введенного им термина: "тропе" по-гречески означает "превращение". К этому корню Клаузиус добавил две буквы – "эн" так, чтобы получившееся слово было бы по возможности подобно слову "энергия". Обе величины настолько близки своей физической значимостью, что известное сходство в их названиях вполне оправдано.
Энтропия, как и энергия, присуща любой термодинамической системе, а не только системе, совершающей цикл Карно.
Напомним, что тепло, отданное системой, мы условились считать отрицательным. С учетом этого равенство (4.44) можно представить в виде:
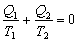 . . |
(4.45) |

Рис. 4.18 |
Обобщим это утверждение, полученное для цикла Карно, на произвольный равновесный круговой процесс, осуществляемый по пути 1а2b'1'.
Проведем ряд бесконечно близких адиабат, пересекающих линии прямого а и обратного b переходов (рис. 4.18). Эти линии разобьются на ряд бесконечно малых отрезков. Через середину каждого отрезка проведем изотермы. Тогда каждую из линий а и b можно считать состоящей из ряда бесконечно близких изотерм. Таким образом, рассматриваемый произвольный цикл представляется совокупностью циклов Карно с переменными температурами нагревателей и холодильников для каждого элементарного цикла.
Обозначим температуры, соответствующие изотермам расширения Т1,
Т2, … Тn, а температуры изотерм на стадии
сжатия – 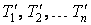 .
Количества теплоты, получаемые системой в процессе расширения на соответствующих
участках элементарных циклов Карно, обозначим
.
Количества теплоты, получаемые системой в процессе расширения на соответствующих
участках элементарных циклов Карно, обозначим  , а количества теплоты, отдаваемые
системой на стадии сжатия –
, а количества теплоты, отдаваемые
системой на стадии сжатия –  .
.
Количества теплоты ΔQi и ΔQ'i (i = 1, 2, … n) система получала соответственно при температурах Ti и отдавала при температурах T'i. Это, следовательно, теплоты изотермических процессов.
На основании равенства (4.45) для каждого элементарного цикла Карно справедливо
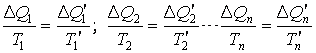 . . |
(4.46) |
 . . |
(4.47) |
 . . |
(4.48) |
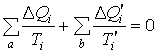 , , |
(4.49) |
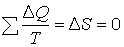 . . |
(4.50) |
Рассмотрим теперь необратимый процесс. Согласно (4.42) имеем:
 , ,или 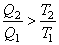 . .
|
(4.51) |
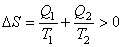 . . |
(4.52) |
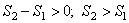 . . |
Таким образом, энтропия изолированной системы тел или остается неизменной при обратимом процессе (ΔS = 0), или возрастает, если система совершает необратимый процесс (ΔS > 0). Следовательно, энтропия изолированной системы тел не может убывать. Это утверждение математически в общем случае может быть записано в виде неравенства:
| ΔS ≥ 0, | (4.53) |
После открытия Клаузиуса стало наконец ясно, почему было так трудно понять связь между теплотой и температурой. Оказалось, что нельзя говорить о количестве теплоты, заключенной в теле. Это понятие просто не имеет смысла. Теплота может переходить в работу, создаваться при трении и, вообще, никакой тенденции к сохранению не имеет.
В то же время точный смысл имеет понятие количества теплоты, переданного телу или же отнятого от него. Теплота может передаваться, но, вообще говоря, не сохраняется. Сохраняющейся величиной в обратимом процессе оказалась совсем новая величина, о существовании которой никто раньше не подозревал, – это и была энтропия Клаузиуса.
Смысл энтропии как функции состояния трудно представить наглядно. Еще Больцман называл ее "чудовищно абстрактной функцией". Однако энтропию можно рассматривать как меру непревратимости, неполноценности, обесцененности внутренней энергии.
Из формул (4.40) и (4.41) следует:
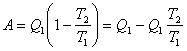 . . |
(4.54) |
 , не может быть превращена в работу.
Эта величина называется связанной энергией. Видно, что она зависит
от отношения
, не может быть превращена в работу.
Эта величина называется связанной энергией. Видно, что она зависит
от отношения  , то есть зависит от энтропии.
Из (4.54) очевидно, что если температура нагревателя Т1 равна температуре
холодильника Т2, то А = 0. Это означает, что если нет тел с различной
температурой, то внутренняя энергия в круговом процессе вообще не может быть использована
для совершения работы. Кроме этого видно, что возрастание энтропии увеличивает связанную
энергию и уменьшает техническую ценность внутренней энергии (ее превращаемость в тепловой
машине в работу).
, то есть зависит от энтропии.
Из (4.54) очевидно, что если температура нагревателя Т1 равна температуре
холодильника Т2, то А = 0. Это означает, что если нет тел с различной
температурой, то внутренняя энергия в круговом процессе вообще не может быть использована
для совершения работы. Кроме этого видно, что возрастание энтропии увеличивает связанную
энергию и уменьшает техническую ценность внутренней энергии (ее превращаемость в тепловой
машине в работу).
Введение энтропии приводит к исключительно важной интерпретации роли энергии в происходящих в природе процессах.
Рассмотрев цикл тепловой машины, мы видим, что с ее помощью можно получить определенную работу, заплатив при этом "налог" в виде теплоты, переданной холодильнику. Энергия, бесполезно ушедшая в холодильник, уже непригодна для совершения работы – если только не воспользоваться еще более холодным холодильником. Следовательно, энергия, запасенная при более высокой температуре, обладает в определенном смысле более высоким качеством, она пригодна для совершения работы, тогда как "качество" энергии, полученной в процессе рассеяния, значительно ниже.
Можно поставить вопрос о качестве энергии, если подойти к нему с позиций энтропии. Допустим, мы отбираем энергию в форме теплоты от нагревателя и позволяем ей перейти непосредственно к холодильнику.
Энтропия нагревателя убывает при этом на величину, равную отношению . . |
 . . |
Итак, возрастание энтропии является характерным признаком естественных процессов. Аналогично можно сказать, что естественное направление процессов изменения характеризуется понижением качества энергии.
Поскольку в промышленно развитом обществе процесс использования энергетических ресурсов стремительно ускоряется, энтропия мира неуклонно возрастает. Следует стремиться не к сохранению энергии, ибо природа делает это автоматически; задача цивилизации заключается в том, чтобы научиться экономно распоряжаться качеством энергии. Необходимы технические решения, направленные на снижение уровня производства энтропии, сущность проблемы заключается в сохранении качества энергии.