Молекулы газа при своем движении постоянно сталкиваются. Скорость каждой молекулы при столкновении изменяется. Она может возрастать и убывать. Однако среднеквадратичная скорость остается неизменной. Это объясняется тем, что в газе, находящемся при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Скорость отдельной молекулы с течением времени может меняться, однако доля молекул со скоростями в некотором интервале скоростей остается неизменной.

Нельзя ставить вопрос: сколько молекул обладает определенной скоростью. Дело в том, что, хоть число молекул очень велико в любом даже малом объеме, но количество значений скорости сколь угодно велико (как чисел в последовательном ряде), и может случиться, что ни одна молекула не обладает заданной скоростью.

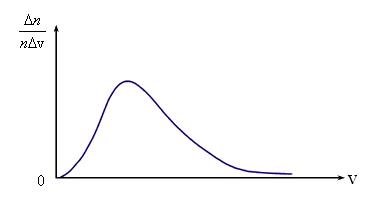
Рис. 3.3

Задачу о распределении молекул по скоростям следует сформулировать следующим образом. Пусть в единице объема n молекул. Какая доля молекул имеет скорости от v₁ до v₁ + Δv? Это статистическая задача.

Основываясь на опыте Штерна, можно ожидать, что наибольшее число молекул будут иметь какую-то среднюю скорость, а доля быстрых и медленных молекул не очень велика. Необходимые измерения показали, что доля молекул , отнесенная к интервалу скорости Δv, т.е. , имеет вид, показанный на рис. 3.3. Максвелл в 1859 г. теоретически на основании теории вероятности определил эту функцию. С тех пор она называется функцией распределения молекул по скоростям или законом Максвелла.

Аналитически она выражается формулой

,

Установление этой зависимости позволило определить кроме уже известной среднеквадратичной скорости еще две характерные скорости – среднюю и наиболее вероятную. Средняя скорость – это сумма скоростей всех молекул, деленная на общее число всех молекул в единице объема.

Средняя скорость, подсчитанная на основании закона Максвелла, выражается формулой

.

.

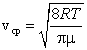1) наиболее вероятную ,

2) среднюю ,

3) среднюю квадратичную 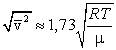, – видим, что наименьшей из них является наиболее вероятная, а наибольшей – средняя квадратичная. Относительное число быстрых и медленных молекул мало (рис. 3.4).

Рис. 3.4

При изменении температуры газа будут изменяться скорости движения всех молекул, а, следовательно, и наиболее вероятная скорость. Поэтому максимум кривой будет смещаться вправо при повышении температуры и влево при понижении температуры. Высота максимума не будет оставаться постоянной. Дело в том, что площадь заштрихованной фигуры численно равна доле общего числа молекул n, которую образуют молекулы со скоростями в указанном интервале. Общая площадь, ограниченная кривой распределения и осью абсцисс (скоростей), таким образом, равна единице и не меняется при изменении температуры (рис. 3.5). Поэтому высота максимума и меняется при изменении температуры.

Рис. 3.5

Кривые распределения молекул по скоростям начинаются в начале координат, асимптотически приближаются к оси абсцисс при бесконечно больших скоростях. Слева от максимума кривые идут круче, чем справа. То, что кривая распределения начинается в начале координат, означает, что неподвижных молекул в газе нет. Из того, что кривая асимптотически приближается к оси абсцисс при бесконечно больших скоростях, следует, что молекул с очень большими скоростями мало. Это легко объяснимо. Для того чтобы молекула могла приобрести при столкновениях очень большую скорость, ей необходимо получить подряд много таких столкновений, при которых она получает энергию, и ни одного столкновения, при котором она ее теряет. А такая ситуация маловероятна.