Выведенное на основании кинетической теории уравнение

.
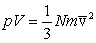позволяет вычислить среднюю квадратичную скорость, которую следует приписать молекулам, чтобы объяснить производимое ими давление. Действительно, в этом уравнении величины р и V легко измеримы, величины же N и m, хотя и неизмеримы непосредственно в отдельности, но произведение их, входящее в формулу, представляет собою массу всех молекул газа, составляющих одну грамм-молекулу, а эта масса, согласно определению грамм-молекулы, численно равна молекулярной массе μ газа.

Так, например, при температуре t = 0º С, то есть при Т = 273 К,

.
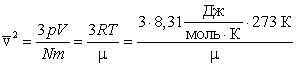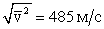Корень квадратный из этой величины и называется средней квадратичной скоростью. Для воздуха, принимая μ = 29 · 10-3 кг/моль,
.
Для водорода, двухатомная молекула которого обладает молекулярной массой,
μ = 2,016 · 10-3 кг/моль,
средняя квадратичная скорость при той же температуре равна 1 840 м/с.

Таким образом, вычисление показало, что средние скорости чрезвычайно велики. Они превышают скорость звука, которая при 0º С равна в воздухе всего 332 м/с. Молекулы в газе летят со скоростью того же порядка, как пуля, вылетающая из винтовки.


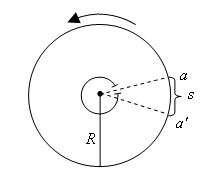
Рис. 3.2

Непосредственное, экспериментальное подтверждение приведенных вычислений было проведено в 1920 г. О. Штерном. В приборе Штерна по оси цилиндрического сосуда располагалась платиновая проволока, покрытая слоем серебра (рис. 3.2). При нагревании проволоки электрическим током серебро испарялось. Молекулы испаряющегося серебра, проходя через щель, достигали стенки цилиндра и создавали в точке а продолговатое серебряное пятно. Затем весь прибор приводился в быстрое вращение вокруг оси, совпадающей с платиновой проволокой. При этом молекулярный пучок серебра отставал, и серебряное пятно оказывалось в месте a'. Смещение s между точками а и a' легко связать со скоростью молекул в пучке.

Пусть радиус цилиндра R. Тогда время t, в течение которого молекулы летят от проволоки до стенки цилиндра, равно

.
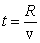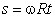За это время t каждая точка на стенке сосуда пройдет путь s, равный
,
где ω – угловая скорость прибора.
Очевидно, что 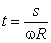. Приравнивая оба выражения для времени, получим:
,
Отсюда .
Найденная величина скорости молекул серебра оказалась равной 600 м/с, что близко к скорости, определяемой по формуле для среднеквадратичной скорости.

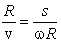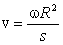В опыте Штерна полоска серебра при неподвижном цилиндре имела резкие края, а при вращающемся – размытые. Это объясняется тем, что не все молекулы имели одну и ту же скорость. Молекулы, имевшие наибольшую скорость, отклонялись меньше, чем медленные. Иначе говоря, в газе скорости молекул при определенной температуре не одинаковы.