В единице объема любого газа при нормальных условиях, то есть при давлении в 1 атм,
что соответствует ~105 Па, и температуре 0º С, что соответствует 273 К,
находится определенное число молекул. Это число легко подсчитать.
Из основного уравнения молекулярно-кинетической теории следует, что
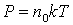 , , |
|
где n0 есть искомое число, k – постоянная Больцмана, надежно
определенная экспериментально.
Итак,
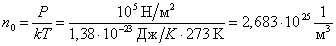 . . |
|
Для большей наглядности найдем число частиц, приходящихся не в 1 м3, а в 1 см3. Тогда получим:
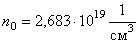 . . |
|
Это означает, что в каждом см3 находится трудно вообразимое число. Если бы в 1 см3 находился бы миллион молекул, то это было бы 106 молекул.
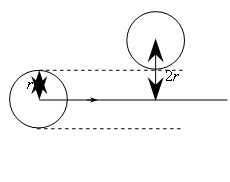
Рис. 3.1 |
Молекулы находятся в газе в состоянии непрерывного хаотического движения, сталкиваются друг с другом. Между столкновениями они проходят свободно путь λ. Длина этого пути между двумя столкновениями различна. Однако можно говорить о средней длине свободного пути – свободном пробеге. Подсчитаем эту величину. Будем считать молекулы газа шариками радиуса r (рис. 3.1). Пусть произвольная молекула движется со скоростью v. После каждого столкновения молекула меняет направление скорости. Однако для простоты предположим, что молекула после столкновения продолжает двигаться в том же направлении, в каком она двигалась до столкновения. Кроме того, для простоты положим, что все другие молекулы, кроме рассматриваемой, неподвижны. Тогда молекула заденет на своем пути все те молекулы, центры которых лежат на расстоянии, не большем 2r от прямой, вдоль которой она движется.
За единицу времени молекула заденет все те молекулы, центры которых лежат внутри
цилиндра радиуса R = 2r и длины l, равной численно скорости молекулы
v. Число молекул z, которые попадают внутрь такого цилиндра, равно
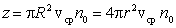 , , |
|
где
n0 – число молекул в единице объема. Число
z и есть число
столкновений в единицу времени. Если учесть движение всех молекул, то более точный расчет
показывает, что
z в
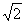
раз больше:
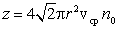 , , |
|
Оценим число соударений, испытываемых молекулой газа в единицу времени. Величина
n0 известна:
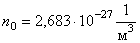 , , |
|
Радиусы молекул определены экспериментально и по порядку величины равны
Средняя скорость
vср ≈ 500 м/с.
Таким образом,
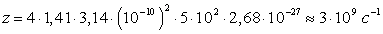 . . |
|
то есть молекула в одну секунду претерпевает миллиарды соударений.
Среднюю длину свободного пробега получим, поделив путь, проходимый за единицу времени, на число столкновений в единицу времени. Так как путь, проходимый в единицу времени, численно равен скорости vcр, то
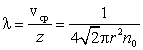 . . |
|
Из этой формулы видно, что с уменьшением давления длина свободного
пробега λ увеличивается. Это происходит из-за того, что n0 прямо
пропорционально давлению газа.
Подсчет средней длины свободного пробега дает для нормальных условий
Это очень маленькая величина.
Для нормальных условий работы электровакуумных приборов (телевизионные трубки, кинескопы и т.п.) необходимо создание высокого вакуума. Высокий вакуум – это не удаление всех молекул из сосуда. Это такое уменьшение давления,
когда λ становится по порядку величины равной характерным размерам сосуда.
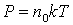 ,
,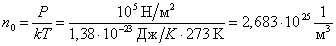 .
.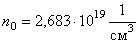 .
.
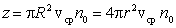 ,
,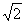 раз больше:
раз больше:
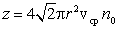 ,
,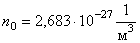 ,
,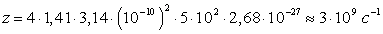 .
.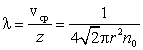 .
.