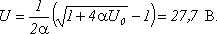|
Тема. Решение задач по теме "Электрическое поле в диэлектриках". Цели: - выяснить, как влияет диэлектрик на основные характеристики электрического поля; - рассмотреть на нескольких примерах методы решения задач, требующих учета влияния диэлектрика на электрическое поле. Ход занятия В ходе проведения занятия необходимо рассмотреть ряд качественных задач и далее решить несколько расчетных задач по мере возрастания их сложности. Прежде чем приступить к выполнению задания, необходимо обсудить, в чем заключается явление поляризации диэлектрика и как это сказывается на характеристиках электростатического поля в веществе, в чем заключаются различия явления электростатической индукции в проводнике и диэлектрике, какой физический смысл имеет диэлектрическая проницаемость. Качественные задачи 1. Металлический заряженный шар окружен толстым сферическим слоем диэлектрика. Нарисуйте картину силовых линий внутри и вне диэлектрика. Укажите причины изменения электрического поля на границе диэлектрика. 2. Положительный и отрицательный точечные заряды притягиваются друг к другу с силой F. Как изменится эта сила, если между зарядами поместить шарик из диэлектрика? 3. Плоский конденсатор, пластины которого велики по сравнению с расстоянием между ними, присоединен к источнику постоянного напряжения. Изменится ли напряженность электрического поля внутри конденсатора, если заполнить пространство между обкладками диэлектриком? 4. Наэлектризованный металлический шарик опустили на дно сухой стеклянной пробирки и поднесли ее к электроскопу. Разойдутся ли листочки электроскопа? 5. Плоский воздушный конденсатор после зарядки отключают от источника напряжения и погружают в керосин. Как изменится энергия, накопленная в конденсаторе? Примеры решения расчетных задач Задача 1. Пространство между обкладками плоского конденсатора заполнено двумя слоями диэлектриков: слоем стекла толщиной d1 = 1 см и слоем парафина толщиной d2 = 2 см. Разность потенциалов между обкладками равна 3000 В. Определите напряженность поля и падение потенциала в каждом из слоев. Диэлектрическая проницаемость стекла Решение: В каждом диэлектрике электрические поля будут однородны. Напряженность поля в каждом слое связана с напряженностью поля в отсутствие диэлектрика соотношениями
Отсюда следует:
Воспользуемся связью разности потенциалов с напряженностью для однородного электрического поля:
Решая совместно (1) и (2), получим:
Ответ: Задача 2. Плоский конденсатор заполнен диэлектриком, и на его пластины подана некоторая разность потенциалов. Его энергия при этом W = 2 Решение: Обозначим через C1 электрическую емкость конденсатора, заполненного диэлектриком, а через С2 электрическую емкость конденсатора, незаполненного диэлектриком. C1 и С2 связаны между собой соотношением C1 =
Отсюда получим U2 = Энергия заполненного конденсатора будет равна
а незаполненного
С другой стороны,
Подставив в последнее выражение W2, получим:
Ответ: Задача 3. Найдите емкость шарового проводника радиусом r, окруженного прилегающим концентрическим слоем диэлектрика с внешним радиусом R и диэлектрической проницаемостью Решение: Емкость проводника определяется отношением заряда q, сообщенного проводнику, к его потенциалу
Потенциал на поверхности шара с зарядом q, окруженного диэлектрическим слоем, будет равен сумме работ по перенесению единичного положительного заряда с поверхности проводника на наружную поверхность диэлектрика и с наружной поверхности диэлектрика на бесконечность
Подставляя найденное значение потенциала в выражение для емкости, получим:
Из последнего соотношения видно, что электроемкость уединенного проводника зависит от его формы, размеров и диэлектрических свойств среды, в которую он погружен. Ответ: Задачи для самостоятельной работы 1. Два заряженных шарика, подвешенных на нитях одинаковой длины, опускают в керосин. Какова должна быть плотность материалов шариков Ответ: 2. Металлический заряженный шар радиуса R поместили в центре диэлектрической сферической оболочки, внутренний и внешний радиусы которой равны соответственно R2 и R3, а относительная диэлектрическая проницаемость Ответ: 
3. Найдите силу натяжения нити F, соединяющей одинаковые шарики радиуса r и массы m каждый, в центре которых находятся одинаковые заряды q. Один из шариков, погрузившись наполовину, плавает на поверхности жидкости с плотностью Ответ: 4. Во сколько раз изменится энергия поля заряженного конденсатора, если пространство между пластинами конденсатора заполнить диэлектриком с диэлектрической проницаемостью 1) конденсатор отключен от источника напряжения; 2) конденсатор остается присоединенным к источнику постоянного напряжения. Ответ объясните, пользуясь законом сохранения энергии. Ответ: 1) уменьшится в 5. Два одинаковых конденсатора соединены последовательно и подключены к источнику электродвижущей силы. Во сколько раз изменится разность потенциалов на одном из конденсаторов, если другой погрузить в жидкость с диэлектрической проницаемостью Ответ: 6. Плоский воздушный конденсатор заряжен до разности потенциалов U = 60 В и отключен от источника электродвижущей силы. После этого внутрь конденсатора вплотную к одной из обкладок вводится пластина из диэлектрика с диэлектрической проницаемостью Ответ: 7. Стеклянная пластина целиком заполняет зазор между обкладками плоского конденсатора, электроемкость которого в отсутствие пластины С = 2 мкФ. Конденсатор зарядили от источника напряжения с электродвижущей силой Ответ: 8. Плоский конденсатор заполнен диэлектриком, проницаемость Ответ: Рекомендуемая литература 1. Бутиков Е.И., Кондратьев А.С. Физика. Т. 2. Электродинамика. Оптика. - М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. - С. 11-86. 2. Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. - М.: Физматлит, 2005. - С. 115-116. 3. Готовцев В.В. Лучшие задачи по электричеству. - М.; Ростов н/Д: Издательский центр "Март", 2004. - С. 5-58. |
 1 = 7, парафина
1 = 7, парафина 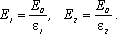
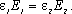 (1)
(1)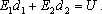 (2)
(2)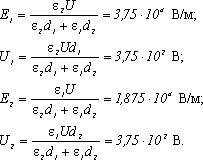

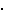 10-5 Дж. После того, как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Работа, которую надо было совершить против сил электрического поля, чтобы вынуть диэлектрик, равна A = 7
10-5 Дж. После того, как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Работа, которую надо было совершить против сил электрического поля, чтобы вынуть диэлектрик, равна A = 7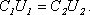
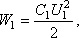
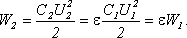
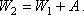
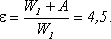
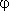 :
: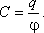
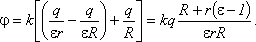
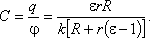
 , чтобы угол расхождения нитей в воздухе и керосине был одинаков? Массы шариков равны. Диэлектрическая проницаемость керосина
, чтобы угол расхождения нитей в воздухе и керосине был одинаков? Массы шариков равны. Диэлектрическая проницаемость керосина 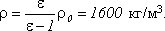
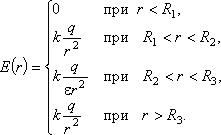
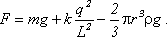
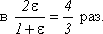

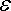 = 1000 В, после чего отключили от него. Найдите механическую работу, которую необходимо совершить против электрических сил, чтобы извлечь пластину из конденсатора. Диэлектрическая проницаемость этого сорта стекла
= 1000 В, после чего отключили от него. Найдите механическую работу, которую необходимо совершить против электрических сил, чтобы извлечь пластину из конденсатора. Диэлектрическая проницаемость этого сорта стекла 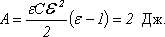
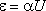 , где
, где 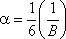 . Параллельно этому нелинейному конденсатору, который первоначально не заряжен, подключают такой же конденсатор, но без диэлектрика, который заряжают до напряжения U0 = 156 В. Определите напряжение U, которое установится между обкладками конденсаторов после завершения переходных процессов.
. Параллельно этому нелинейному конденсатору, который первоначально не заряжен, подключают такой же конденсатор, но без диэлектрика, который заряжают до напряжения U0 = 156 В. Определите напряжение U, которое установится между обкладками конденсаторов после завершения переходных процессов.