|
Тема. Решение задач по теме «Неинерциальные системы отсчета». Цели: - рассмотреть силы инерции, которые вводятся для описания движения в неинерциальных системах отсчета, движущихся поступательно с ускорением или вращающихся относительно инерциальных систем отсчета; - показать на нескольких примерах методы решения задач в неинерциальных системах отсчета.
Ход занятия Прежде чем приступить к выполнению задания, следует рассмотреть на примере качественных задач два типа неинерциальных систем отсчета: - системы, движущиеся относительно какой-либо инерциальной системы отсчета, например Земли, прямолинейно и ускоренно; - системы, вращающиеся с постоянной угловой скоростью относительно какой-либо инерциальной системы отсчета.
Качественные задачи 1. Можно ли в вагоне движущегося поезда с помощью отвеса обнаружить наклон железнодорожного полотна на повороте? 2. Пусть система отсчета, связанная с Землей, является инерциальной. Можно ли считать инерциальной систему отсчета, связанную с автомобилем, если он а) движется равномерно по прямолинейному участку шоссе; б) разгоняется по прямолинейному участку шоссе; в) движется равномерно по извилистой дороге; г) по инерции вкатывается на гору. 3. Закрытый фонарь со свечой движется прямолинейно с ускорением. Можно заметить, что при этом пламя наклоняется в направлении ускорения движения. Как объяснить явление? 4. Куда отклонится пламя свечи в фонаре, находящемся на вращающейся карусели? 5. Автомобиль делает резкий поворот. Пассажир, сидящий у правой стенки, оказался прижатым к ней. В какую сторону сделал поворот автомобиль? 6. Почему в северном полушарии река подмывает правые берега? 7. В какую сторону будет смещаться относительно Земли реактивный снаряд, пущенный вдоль меридиана?
Задача 1. Тело
находится в покое на вершине наклонной плоскости (рис. 1). За какое время
тело соскользнет с плоскости, если плоскость в момент времени t = 0 начнет двигаться влево в
горизонтальном направлении с ускорением а = 1 м/с2?
Длина плоскости Систему отсчета удобно связать с наклонной плоскостью. Но плоскость движется с ускорением по отношению к Земле. Для рассматриваемого движения Земля является инерциальной системой отсчета. Следовательно, система отсчета, связанная с наклонной плоскостью, неинерциальна, и в уравнении движения тела необходимо ввести поступательную силу инерции.
где Спроецируем уравнение (1) на ось Х, направленную вдоль наклонной плоскости, и перпендикулярную к ней ось Y.
Учитывая, что
Так как ускорение
Ответ:
Решение: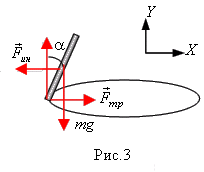
Считаем мотоциклиста и мотоцикл единым телом. На него
действуют: сила тяжести Будем полагать,
что линейные размеры мотоциклиста много меньше радиуса окружности, а значит,
все точки тела будут двигаться с одинаковым ускорением. Тогда центробежная сила
инерции определится выражением
где
Чтобы найти
Спроецируем это равенство на горизонтальную ось Х, направленную к центру окружности, и вертикальную ось Y.
Отсюда
Подставим полученные выражения в (2), тогда получим
Чтобы найти максимальное значение скорости, с которой может ехать велосипедист, воспользуемся тем, что максимальное значение силы трения покоя
Проскальзывания не будет, если
или
Таким образом,
Ответ:
Задача 3. Два шарика, связанных нитью, могут скользить по гладкому стержню. Каково отношение масс шариков, если при их вращении они остаются в равновесии, когда один из них находится на расстоянии R1 = 7 см, а второй на расстоянии R2 = 14 см от оси вращения? Решение: Будем решать задачу в системе отсчета, связанной со стержнем. Шарики относительно стержня покоятся. Такая система отсчета является неинерциальной: она вращается относительно Земли. Поэтому на каждый шарик в горизонтальном направлении помимо силы натяжения нити будет действовать центробежная сила инерции.
где
Следовательно,
Ответ:
Задача 4. Куб, наполовину заполненный водой, двигают горизонтально с ускорением а. Найдите угол наклона жидкости к горизонту. Решение:
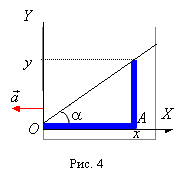
Выберем два очень узких столбика жидкости – вертикальный и горизонтальный. На рис. 4 они показаны заштрихованными полосками. Так как эти столбики неподвижны, то результирующая сила, действующая на каждый столбик, равна нулю. На вертикальный столбик вдоль оси Y действует сила тяжести и силы давления на верхнее и нижнее основание. Поэтому условие его равновесия запишется так:
где На горизонтальный столбик вдоль оси X действуют силы давления и поступательная сила инерции. Условие равновесия этого столбика имеет вид:
где Массы столбиков будут равны: Подставим значения
Сложив два последних соотношения, получим
Отсюда
Ответ:
1. Наклонная
плоскость с углом наклона Ответ:
Ответ:
3. Муфточка
А может свободно скользить вдоль
гладкого стержня, изогнутого в форме полукольца радиуса R (рис. 6).
Систему привели во вращение с постоянной угловой скоростью Ответ:
если
4.
Через блок, прикрепленный к потолку кабины лифта, перекинута нить, к концам
которой привязаны грузы с массами а) ускорение груза б) силу Ответ:
Рекомендуемая литература 1. Физика. Механика / Под ред. Г.Я. Мякишева. – М.: Просвещение, 1995. – С. 245–259. 2. Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. – М.: Физматлит, 2005. – С. 63–67. 3. Готовцев В.В. Лучшие задачи по механике и термодинамике. – М.; Ростов н/Д: Издательский центр «Март», 2004. – С. 184–212. |
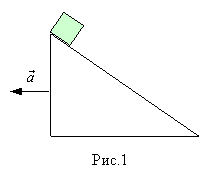
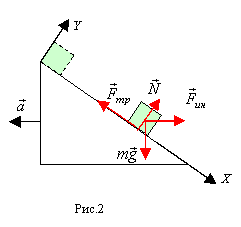 Таким образом, на движущееся тело в системе
отсчета, связанной с наклонной плоскостью, действуют четыре силы: сила тяжести
Таким образом, на движущееся тело в системе
отсчета, связанной с наклонной плоскостью, действуют четыре силы: сила тяжести 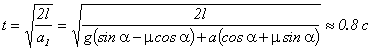 .
.
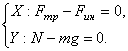
 Выберем в качестве тела
отсчета куб. Такая система отсчета будет неинерциальной. Она движется
поступательно с ускорением
Выберем в качестве тела
отсчета куб. Такая система отсчета будет неинерциальной. Она движется
поступательно с ускорением 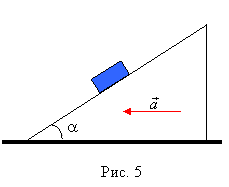 Задачи для самостоятельной работы
Задачи для самостоятельной работы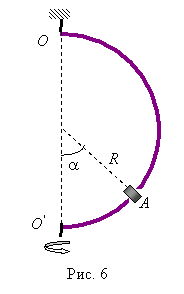 2. На поверхности Земли на широте
2. На поверхности Земли на широте