|
Тема. Решение задач по теме «Работа, мощность, энергия, закон сохранения энергии». Цели: - на примере конкретных задач рассмотреть понятия работы, потенциальной кинетической энергии; - проанализировать границы применимости законов сохранения на конкретных примерах. Ход занятия В ходе проведения занятия учащимся предлагается несколько задач по возрастанию сложности. В большинстве интересных случаев при решении задач приходится использовать как закон сохранения импульса, так и закон сохранения механической энергии. Если для решения задачи достаточно одного закона сохранения, следует обсудить выполняется ли второй закон сохранения, а если не выполняется, то по какой причине. Для решения задачи рекомендуется выполнить следующие действия. - Выбрать тела, которые Вы включите в систему, для которой будете использовать законы сохранения. - Выбрать систему отсчета, в которой будете решать задачу. Убедиться, что она является инерциальной. Удачный выбор системы отсчета, как и при решении задач кинематики и динамики, может существенно облегчить составление системы уравнений в случае использования законов сохранения. Не забывайте, что при переходе из одной инерциальной системы отсчета в другую перемещения и скорости тел меняются, а поэтому работа и кинетическая энергия будут зависеть от выбора системы отсчета. Потенциальная же энергия зависит от относительных координат взаимодействующих тел, следовательно, она одинакова во всех инерциальных системах отсчета. - Выбрать начальное и конечное состояния системы, которые Вы свяжете законами сохранения. Следует иметь в виду, что эти состояния совсем необязательно должны совпадать с начальным и конечным состояниями, указанными в условии задачи. - Обосновать возможность использования законов сохранения для выбранных состояний системы. - Выбрать начало отсчета потенциальной энергии. Целесообразно за нуль отсчета потенциальной энергии выбрать положение, в котором она минимальна в рассматриваемой задаче. Помните, что если тело нельзя считать материальной точкой, то его потенциальная энергия в поле силы тяжести определяется положением центра масс этого тела. - Записать значения импульса тела или его механической энергии в начальном и конечном положениях и приравняйте их. - Если законов сохранения окажется недостаточно для решения задачи, использовать уравнения динамики и кинематические соотношения. - Обратить внимание на то, что если физическая система не является замкнутой и внутри нее не действуют непотеннциальные силы, то изменение ее механической энергии равно работе внешних сил. Если система является замкнутой, но внутри системы действуют непотенциальные силы, полная механическая энергия не сохраняется. Изменение механической энергии в этом случае равно работе непотенциальных сил. В частности, механическая энергия не сохраняется при неупругом ударе. Качественные задачи 1. В каком случае расходуется меньше энергии при запуске спутника Земли: при запуске вдоль меридиана или вдоль экватора в сторону вращения Земли? 2. Два одинаковых тела падают с высоты H: одно в воздухе, другое – в вакууме. Одинаковы ли потенциальные энергии тел в начале падения? Одинаковы ли их кинетические энергии в конце падения? 3. Шофер автомобиля, едущего со скоростью v, внезапно увидел перед собой на расстоянии a широкую стену. Что ему выгоднее: затормозить или повернуть? 4. И свинец, и тяжелая вода практически не поглощают нейтроны. Почему же в атомных реакторах для торможения нейтронов тяжелую воду используют, а свинец – нет? 5. Как будут двигаться два одинаковых шарика после центрального упругого удара в отсутствие внешних сил, если один из них до удара покоился? 6. Почему при попадании пули в баллистический маятник нельзя применять закон сохранения механической энергии ко всему процессу в целом? Примеры решения расчетных задач Задача 1. Цепочка
длиной Решение: 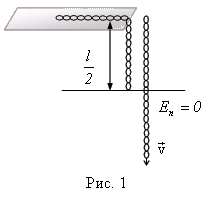
Поскольку при движении цепочки сила трения отсутствует, то полная механическая энергия системы будет сохраняться. В качестве начального состояния выбираем цепочку в начальный момент времени, конечного – в момент, когда ее верхний конец соскользнет со стола. Будем считать потенциальную энергию цепочки в конечном состоянии равной нулю (рис. 1). Величина потенциальной энергии определяется положением центра массы тела. Поэтому в начальном состоянии полная механическая энергия системы
В конечном состоянии полная механическая энергия Ответ:
Задача 2.
Человек массы m переходит с одного конца лодки массой М на
другой. Длина лодки равна Решение: Поскольку система «лодка–человек» является замкнутой, то для решения задачи можно использовать закон сохранения импульса. В качестве тела отсчета выберем Землю. В начальный момент времени импульс системы «лодка–человек» равен нулю, следовательно, он будет таковым и во все последующие моменты времени:
где Согласно закону сложения скоростей
Из последнего выражения
Обозначим время движения человека через t, тогда перемещение лодки относительно берега будет равно
где Ответ: Задача 3. Две частицы массой m скреплены пружиной жесткости k. На них налетает третья частица массы m, которая движется вдоль оси пружины со скоростью v. Найдите максимальное сжатие пружины. Внешними силами пренебречь. Решение: Разобьем процесс взаимодействия частиц и пружины на две стадии (рис. 2) 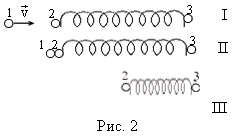
1. За состояние I примем исходное состояние системы: частица
1 движется со скоростью
где
Чтобы
эти уравнения были совместны, необходимо, чтобы 2. На второй стадии в начальном состоянии движется со
скоростью
где х – максимальное сжатие пружины. Решая эту систему уравнений, получим
Ответ: Задача 4. Пуля, летящая горизонтально со скоростью v= 400 м/с, попадает в подвешенный на невесомой нити брусок и застревает в нем. Какова длина нити, если брусок отклонился на угол a = 60°? Масса пули m = 20 г, масса бруска М = 5 кг. Решение: 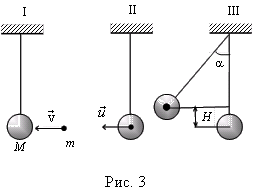
Если за начальное состояние системы «шар–пуля» выбрать летящую пулю, а за конечное – отклонившийся брусок с застрявшей в нем пулей, то нельзя воспользоваться ни законом сохранения импульса (так как система «шар–пуля» не является замкнутой), ни законом сохранения механической энергии (так как соударение пули с шаром неупругое). Чтобы
воспользоваться законами сохранения, следует рассмотреть промежуточное
состояние II (рис. 3): пуля вошла в шар и застряла
в нем, но поскольку время соударения очень мало, то сам шар практически не
сдвинулся с места, хотя и приобрел скорость
Закон сохранения импульса записан в скалярном виде, так как импульс в начальном и конечном состоянии направлен одинаково. При переходе шара с застрявшей в нем пулей из состояния II в состояние III можно воспользоваться законом сохранения механической энергии. Будем отсчитывать потенциальную энергию взаимодействия шара с Землей от центра масс шара, находящегося в положении равновесия. Тогда
Из геометрических соображений ясно, что
Решая совместно (2)–(4), получим
Ответ: Задача 5. Пять одинаковых шаров,
центры которых лежат на одной прямой, находятся на небольшом расстоянии друг от
друга. В крайний шар ударяется такой же шар, имеющий скорость Решение: При столкновении двух одинаковых шаров движущийся шар останавливается, а покоящийся приобретает его скорость. Поэтому после последовательных столкновений все шары будут покоиться, кроме последнего, который приобретет скорость v = 20 м/с. Ответ: скорость последнего шара v = 20 м/с. Задача 6. Четыре одинаковых тела
равной массы по m = 20 г
каждое расположены на одной горизонтальной прямой на некотором расстоянии друг
от друга. В крайнее тело ударяется такое же тело, имеющее скорость Решение: Так как удар неупругий, то полная механическая энергия системы тел не сохраняется. Но будет сохраняться полный импульс системы, то есть
следовательно, вся система слипшихся шаров будет двигаться со скоростью
а ее кинетическая энергия будет равна
Ответ:
Решение: Так как горка стоит на гладкой поверхности, то при движении тела массой m вниз горка будет двигаться влево. Непотенциальные силы отсутствуют, следовательно, будет сохраняться полная механическая энергия этой системы. Будем отсчитывать потенциальную энергию от основания горки. За начальное состояние примем тело на высоте Н. В этот момент горка и тело неподвижны. В конечном состоянии в момент схода с горки тело находится на высоте h и движется со скоростью v, а горка движется влево со скоростью U. Потенциальная энергия горки остается неизменной. Исходя из вышесказанного, закон сохранения механической энергии будет иметь вид
Поскольку в конце движения тело движется по горизонтали, и результирующая сила, действующая на него равна нулю, то будет выполняться закон сохранения импульса. Для выбранных начального и конечного состояний он запишется следующим образом:
Проецируя это выражение на ось х, получим
Из уравнений (5) и (6) можно найти скорости тела и горки в момент схода тела.
Чтобы найти расстояние от тела до горки в момент падения, перейдем в систему отсчета, связанную с горкой. В этой системе отсчета тело будет двигаться по параболе с начальной скоростью U + v, направленной горизонтально. Пройденное им расстояние по вертикали будет равно
где t – время движения тела до приземления. Его можно определить, если принять во внимание, что тело движется по вертикали с ускорением свободного падения, следовательно,
Отсюда искомое расстояние S будет равно
Ответ: Задача 8. Колодец, площадь дна которого S, а глубина Н, наполовину заполнен водой. Насос выкачивает воду и подает ее на поверхность земли через цилиндрическую трубу радиуса R. Какую работу А совершит насос, если выкачивает всю воду из колодца за время t? Решение: Работа, затрачиваемая
на подъем воды из колодца, равна изменению механической энергии воды.
Потенциальная энергия воды в колодце определяется положением центра масс воды,
который находится на расстоянии
где r – плотность воды. Кроме того, насос сообщает воде кинетическую энергию. Скорость v, с которой вода вытекает из трубы, можно определить из соотношения
Отсюда
И, наконец, работа, затраченная на подъем воды, будет равна
Ответ:
Задачи для самостоятельной работы 1. На
тело действуют две силы Ответ: 2. Стоящий
на льду человек массой M = 60 кг ловит мяч массой m = 0,5 кг, который летит горизонтально со
скоростью Ответ: 3. Человек на Земле прыгает
на высоту Ответ: 4. Тело
массой Ответ: 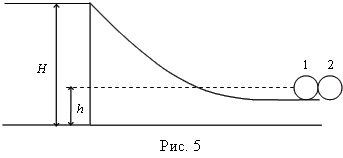
5. Шарик массой m соскальзывает по желобу, имеющему на конце горизонтальный участок с высотой Н = 1,4 м. В конце желоба он сталкивается с таким же шариком, установленным на подставке на высоте h = 0,7 м (рис. 5). Считая удар абсолютно упругим, определите дальность полета второго шарика. Ответ: 6. На
конце соломинки, лежащей на гладком столе, сидит маленький кузнечик массы m. С какой наименьшей скоростью относительно неподвижного
наблюдателя должен прыгнуть кузнечик, чтобы попасть на другой конец соломинки? Масса
соломинки М, ее длина Ответ: 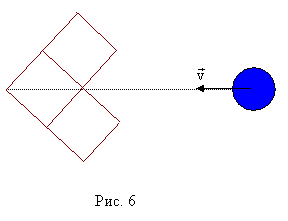
7. На группу из трех гладких одинаковых кубиков, лежащих на гладкой горизонтальной поверхности, как показано на рисунке, налетает со скоростью v гладкая шайба (рис. 6). Масса каждого кубика равна массе шайбы. Диаметр шайбы и ее высота равны ребру кубика. Определите скорости всех тел после соударения. Ответ: после удара шайба останавливается,
средний кубик остается неподвижным, крайние кубики будут двигаться со скоростью
8. Груз
массой Ответ: 9. Веревка
длины Ответ: движение
веревки не будет равноускоренным.
Ответ: Рекомендуемая литература 1. Бутиков Е.И., Кондратьев А.С. Физика. Т. 1. Механика. – М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. – С. 164–260. 2. Физика. Механика / Под ред. Г.Я. Мякишева. – М.: Просвещение, 1995. – С. 260–363. 3. Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. – М.: Физматлит, 2005. – С. 46–55. 4. Готовцев В.В. Лучшие задачи по механике и термодинамике. – М.; Ростов н/Д: Издательский центр «Март», 2004. – С. 148–177. |
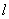 лежит
на гладком горизонтальном столе, свешиваясь ровно наполовину. Цепочку без
толчка отпускают. Найдите скорость цепочки в момент, когда ее верхний конец
соскользнет со стола.
лежит
на гладком горизонтальном столе, свешиваясь ровно наполовину. Цепочку без
толчка отпускают. Найдите скорость цепочки в момент, когда ее верхний конец
соскользнет со стола. 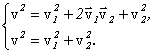
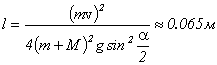 .
.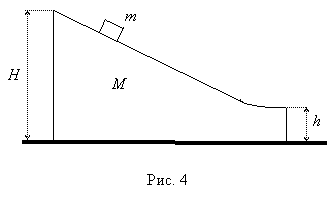 Задача 7. Горка массой М,
расположенная на гладкой плоскости, имеет горизонтальный участок. На горку
положили тело массой m и отпустили с высоты H (рис. 4). Каким будет
расстояние от тела до горки, когда оно упадет? Высота, с которой падает тело,
соскользнув с горки – h. Трение отсутствует.
Задача 7. Горка массой М,
расположенная на гладкой плоскости, имеет горизонтальный участок. На горку
положили тело массой m и отпустили с высоты H (рис. 4). Каким будет
расстояние от тела до горки, когда оно упадет? Высота, с которой падает тело,
соскользнув с горки – h. Трение отсутствует.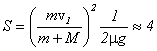 см.
см.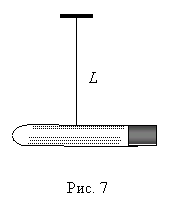 10. В
пробирке массы M, закрытой пробкой массы m, находится капля эфира. При нагревании пробирки пробка
вылетает под давлением паров эфира. Пробирка подвешена на невесомом жестком
стержне длины L (рис. 7). С какой
минимальной скоростью должна вылететь пробка, чтобы пробирка сделала полный
оборот вокруг точки подвеса?
10. В
пробирке массы M, закрытой пробкой массы m, находится капля эфира. При нагревании пробирки пробка
вылетает под давлением паров эфира. Пробирка подвешена на невесомом жестком
стержне длины L (рис. 7). С какой
минимальной скоростью должна вылететь пробка, чтобы пробирка сделала полный
оборот вокруг точки подвеса?