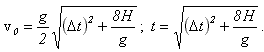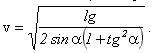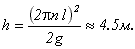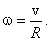|
Тема. Решение задач по теме "Кинематика материальной точки". Цели:
Ход занятия Последовательность действий при решении кинематических задач определяется необходимостью записать основные уравнения теории применительно к условиям конкретной задачи. Для этого следует:
Качественные задачи
Примеры решения расчетных задач 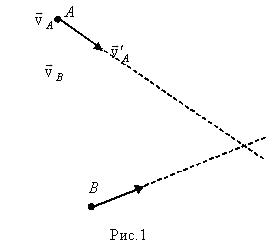
Задача 1. Две машины А и В идут пересекающимися курсами (рис. 1) с заданными скоростями Решение: Скорости 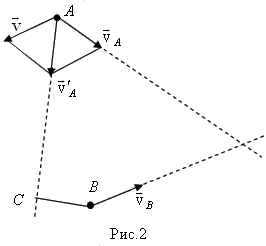
Машина будет неподвижна в системе отсчета, связанной с этой машиной. Пусть система отсчета связана с машиной В. Тогда, согласно закону сложения скоростей, скорость машины А в системе отсчета, связанной с машиной В, будет складываться из скорости машины А относительно Земли Ответ: наименьшее расстояние, на которое сближаются машины, равно BC. 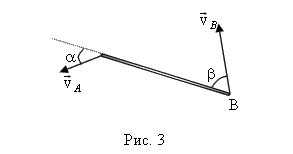
Задача 2. Жесткий стержень движется в плоскости так, что скорость точки А стержня равна Решение: В системе отсчета, связанной с плоскостью, в которой движется стержень, его движение выглядит очень сложно: оно складывается из поступательного и вращательного движения. Задача сильно упростится, если систему отсчета связать с точкой А. В этой системе отсчета точка В будет двигаться по окружности, а значит скорость этой точки 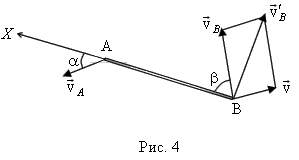
Векторное равенство (1) целесообразно спроецировать на ось X, направленную вдоль стержня. Тогда получим Ответ: Задача 3. Концы стержня А и В скользят по сторонам прямого угла (рис. 5). Как зависит от угла α ускорение середины стержня С, если конец В движется с постоянной скоростью Решение: 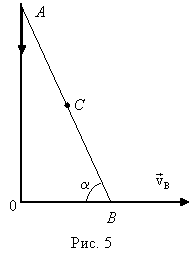
В системе отсчета, связанной с Землей, точка А стержня будет двигаться вдоль вертикальной стороны прямого угла. Обозначим эту скорость (2)
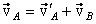 . .
Так как (3)
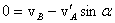 . . В системе отсчета, связанной с точкой В, нормальное ускорение точки А 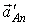 будет направлено вдоль стержня и равно по величине будет направлено вдоль стержня и равно по величине 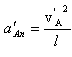 . Так как . Так как 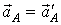 , то , то 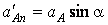 . Следовательно, . Следовательно, 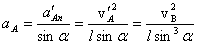 . . 
Из закона сложения скоростей следует, что ускорения в точке С будут одинаковыми в обеих системах отсчета Ответ: 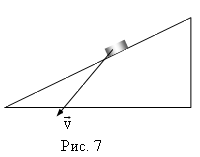
Задача 4. Скорость монеты Решение: При движении монеты вдоль клина сам клин будет скользить по горизонтальной плоскости вправо со скоростью Задача 5. Даны три бильярдных стола разной длины, но одинаковой ширины. От длинных бортов бильярдов одновременно посылаются шары с одинаковой по модулю и направлению скоростью. Одновременно ли вернутся шары после всех возможных отражений к тому же борту? Считать удар шара о борт бильярда абсолютно упругим. Решение: Возможные случаи движения шаров изображены на рис. 9. Движение шара происходит во всех случаях в плоскости стола, поэтому это движение можно представить в виде суммы движений вдоль длинной и короткой сторон стола. Ответ: шары вернутся к борту, от которого начиналось их движение, одновременно. Задача 6. Бильярдный шар находится в точке А. Размеры бильярда и расстояние шара от лузы В даны на рис. 10а. Под каким углом к короткому борту надо направить шар, чтобы попасть в лузу В после отражения шара от двух бортов? Считать, что удар шара о борт является абсолютно упругим, то есть угол падения равен углу отражения. Решение: Траектория, по которой будет двигаться шар, показана на рис. 10б. Шар движется в плоскости стола, Ответ: Задача 7. Два тела движутся по прямой навстречу друг другу с начальными скоростями v1 и v2 и постоянными ускорениями a1 и a2, направленными противоположно соответствующим скоростям в начальный момент времени. При каком максимальном расстоянии между телами они встретятся в процессе движения? Решение: В системе отсчета, связанной с Землей, встреча двух тел может произойти либо при их движении навстречу друг другу, либо, если одно из тел изменило направление движения раньше, чем произойдет встреча, а другое тело его догонит. Задачу удобно решать в системе отсчета, связанной с одним из движущихся тел. Тогда в момент встречи скорость второго тела должна обратиться в нуль. Скорость в начальный момент времени и ускорение движущегося тела будут соответственно равны v1 + v2 и a1 + a2. Момент времени, когда произошла встреча, определится из условия, что скорость движущегося тела в этот момент обращается в нуль: (4)
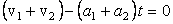 . .
Так как ускорение постоянно, то максимальное расстояние будет равно (5)
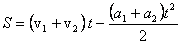 . .
Решая совместно (4) и (5), получим 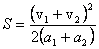 . .
Ответ: Задача 8. С башни высотой Н под углом α к горизонту (вниз) бросают тело. Одновременно с поверхности Земли под углом α к горизонту бросают второе тело навстречу первому. Определите, на каком расстоянии от подножия башни находится место бросания второго тела, если оба тела столкнулись в воздухе. 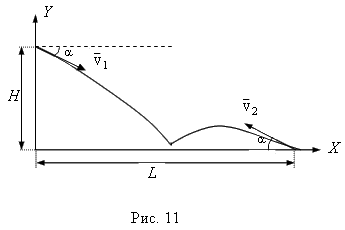
Решение: Поскольку оба тела движутся в одной плоскости, то движение каждого из них можно представить в виде суммы независимых движений по горизонтали и вертикали. Выберем в качестве тела отсчета Землю. И с телом отсчета свяжем систему координат, имеющую две оси X и Y, начало которой находится у подножия башни (рис. 11). Так как оба тела движутся под действием силы тяжести, направленной вертикально вниз, то движение по горизонтали будет равномерным, а по вертикали тела будут двигаться с постоянным ускорением, равным ускорению свободного падения. Обозначим скорость первого тела в начальный момент времени
Поделив первое уравнение на второе, получим Ответ: Задача 9. Мальчик держит один конец доски, а другой ее конец лежит на цилиндре (рис. 12). Решение: Если тело одновременно участвует во вращательном и поступательном движении, то для описания его движения удобно ввести мгновенную ось. Тогда тело в каждый момент времени будет поворачиваться относительно мгновенной оси как целое. Для цилиндра такой мгновенной осью является его образующая О, касающаяся плоскости, по которой он катится (рис. 13).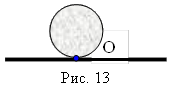 Угловая скорость всех точек колеса относительно оси О будет одинаковой. Следовательно, линейная скорость точки, в которой доска соприкасается с цилиндром, будет в 2 раза больше линейной скорости, с которой движется ось цилиндра. Поэтому к тому времени, когда мальчик пройдет расстояние L, ось цилиндра переместится на расстояние L/2. Таким образом, чтобы дойти до цилиндра, мальчик должен пройти расстояние 2L. Угловая скорость всех точек колеса относительно оси О будет одинаковой. Следовательно, линейная скорость точки, в которой доска соприкасается с цилиндром, будет в 2 раза больше линейной скорости, с которой движется ось цилиндра. Поэтому к тому времени, когда мальчик пройдет расстояние L, ось цилиндра переместится на расстояние L/2. Таким образом, чтобы дойти до цилиндра, мальчик должен пройти расстояние 2L.
Ответ: мальчик должен пройти расстояние 2L. Задачи для самостоятельной работы 1. Автомобиль и мотоцикл движутся навстречу друг другу со скоростями соответственно равными 12 м/с и 24 м/с. Расстояние между ними в начальный момент времени равно 500 м. Считая, что автомобиль и мотоцикл движутся вдоль оси Х, направленной в сторону движения автомобиля, запишите закон движения х(t) для автомобиля и мотоцикла. В начальный момент времени положение автомобиля совпадает с началом отсчета, и он движется в положительном направлении оси Х. Ответ: x1=12t; x2=500-24t 2. Из двух городов навстречу друг другу выехали два автобуса: один в 9 ч., другой в 9 ч. 30 мин. Первый двигался со скоростью 40 км/ч, второй - 60 км/ч. Длина пути равна 120 км. В какое время и на каком расстоянии от городов встретились автобусы? Ответ: встреча произошла в 10 ч. 30 мин. на середине пути. 3. Пассажир поезда, идущего со скоростью 40 км/ч, видит в течение 3 с встречный поезд длиной 75 м. С какой скоростью идет встречный поезд? Ответ: v = 50 км/ч. 4. Колесо радиусом R = 10 см вращается так, что зависимость линейных скоростей точек, лежащих на ободе колеса, дается уравнением v=At+Bt2, где А = 0,5 см/с2, В = 1 см/с3. Найдите угол α, составляемый вектором полного ускорения с радиусом колеса в момент времени t = 2,4 c после начала движения. Ответ: α=48'. 5. Тело бросают вертикально вверх. Промежуток времени между двумя моментами, когда тело проходит точку, находящуюся на высоте Н, равен Ответ: 6. По двум пересекающимся под углом 30° дорогам движутся два автомобиля: один со скоростью 54 км/ч, второй - со скоростью 26 км/ч. Через минуту после пересечения первым автомобилем перекрестка по другой дороге его пересек второй автомобиль. Определите наименьшее расстояние между автомобилями после пересечения перекрестка вторым автомобилем. Ответ: 0,78 км. 7. Камень бросают горизонтально с вершины горы, имеющей угол наклона, равный α. С какой скоростью v должен быть брошен камень, чтобы он упал на расстоянии l (вдоль наклонной плоскости) от вершины? Сопротивлением воздуха можно пренебречь. Ответ: 8. Радиус рукоятки колодезного ворота в три раза больше радиуса вала, на который наматывается трос. Какова линейная скорость конца рукоятки при поднятии ведра с глубины 10 метров за 20 секунд? Ответ: v = 1,6 м/с. 9. Мальчик вращает камень, привязанный к веревке длиной l=0.55м в вертикальной плоскости, делая число оборотов n=3об/с. На какую высоту взлетел камень, если веревка оборвалась в тот момент, когда скорость была направлена вертикально вверх? Ответ: 10. Колесо радиусом 50 см равномерно катится со скоростью 18 км/ч. Какова величина скорости v верхней точки колеса? Ответ: v=10 м/с. 
11. Обруч бросают на шероховатую горизонтальную плоскость с линейной скоростью v. Одновременно ему сообщают вращательное движение в таком направлении, что он должен катиться по плоскости в ту же сторону (рис. 14). При какой угловой скорости ω обруч покатится по плоскости без скольжения, если радиус обруча R? Ответ: Рекомендуемая литература 1. Бутиков Е.И., Кондратьев А.С. Физика. Т. 1. Механика. - М.: Физматлит: Лаборатория базовых знаний; СПб.: Невский диалект, 2001. - С. 11-82. 2. Физика. Механика / Под ред. Г.Я. Мякишева. - М.: Просвещение, 1995. - С. 3-135. 3. Белолипецкий С.Н., Еркович О.С., Казаковцева В.А. и др. Задачник по физике. - М.: Физматлит, 2005. - С. 9-30. 4. Готовцев В.В. Лучшие задачи по механике и термодинамике. - М.; Ростов н/Д: Издательский центр "Март", 2004. - С. 5-71. |
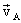 и
и  . Определите графически наименьшее расстояние, на которое сближаются машины.
. Определите графически наименьшее расстояние, на которое сближаются машины.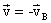 , с которой Земля движется относительно машины В (рис. 2). Скорость машины А в системе отсчета, связанной с машиной В, находим по правилу сложения векторов. Искомое минимальное расстояние равно ВС.
, с которой Земля движется относительно машины В (рис. 2). Скорость машины А в системе отсчета, связанной с машиной В, находим по правилу сложения векторов. Искомое минимальное расстояние равно ВС. будет перпендикулярна стержню (рис. 4). Согласно закону сложения скоростей
будет перпендикулярна стержню (рис. 4). Согласно закону сложения скоростей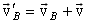 , (1)
, (1)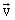 - скорость, с которой плоскость движения стержня движется относительно точки А,
- скорость, с которой плоскость движения стержня движется относительно точки А, 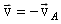 .
.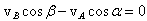 , откуда
, откуда 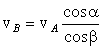 .
.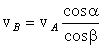 .
.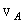 . Перейдем к системе отсчета, связанной с одним из концов стержня - с точкой В. В этой системе отсчета точка А будет вращаться по окружности с изменяющейся скоростью
. Перейдем к системе отсчета, связанной с одним из концов стержня - с точкой В. В этой системе отсчета точка А будет вращаться по окружности с изменяющейся скоростью 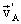 , перпендикулярной к стержню (рис. 6). Согласно закону сложений скоростей
, перпендикулярной к стержню (рис. 6). Согласно закону сложений скоростей , то ускорение точки А будет одинаковым в обеих системах отсчета. Спроецируем векторное равенство (2) на ось X. Тогда получим
, то ускорение точки А будет одинаковым в обеих системах отсчета. Спроецируем векторное равенство (2) на ось X. Тогда получим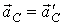 . Так как все точки стержня движутся с одной и той же угловой скоростью, а линейная и угловая скорости связаны соотношением
. Так как все точки стержня движутся с одной и той же угловой скоростью, а линейная и угловая скорости связаны соотношением 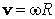 , где R - радиус окружности, по которой движется точка, то
, где R - радиус окружности, по которой движется точка, то 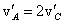 . Следовательно, нормальное и тангенциальное ускорения в точке С будут в два раза меньше по модулю, чем в точке А, и
. Следовательно, нормальное и тангенциальное ускорения в точке С будут в два раза меньше по модулю, чем в точке А, и 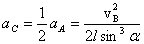 .
.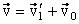 , где
, где 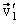 - скорость движения монеты относительно клина,
- скорость движения монеты относительно клина, 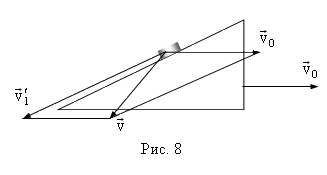 направленная вдоль наклонной плоскости. Следовательно, вектор
направленная вдоль наклонной плоскости. Следовательно, вектор  и
и  , что и дает возможность найти
, что и дает возможность найти 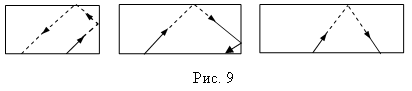 Все шары в начальный момент времени имеют одинаковые составляющие скорости, параллельные короткому борту. При ударе о короткий борт эта составляющая не меняется, а при ударе о длинный - меняет направление, но ее величина остается постоянной. Так как ширина всех бильярдов одинакова, все три шара вернутся к тому борту, от которого начиналось их движение, одновременно.
Все шары в начальный момент времени имеют одинаковые составляющие скорости, параллельные короткому борту. При ударе о короткий борт эта составляющая не меняется, а при ударе о длинный - меняет направление, но ее величина остается постоянной. Так как ширина всех бильярдов одинакова, все три шара вернутся к тому борту, от которого начиналось их движение, одновременно.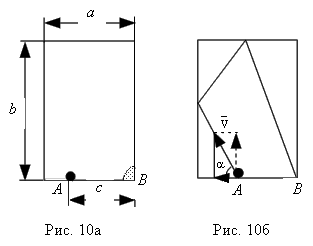 поэтому его движение можно рассматривать как сумму независимых движений вдоль длинного и вдоль короткого борта. Обозначим скорость шара в начальный момент времени через
поэтому его движение можно рассматривать как сумму независимых движений вдоль длинного и вдоль короткого борта. Обозначим скорость шара в начальный момент времени через 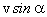 , а вдоль короткого -
, а вдоль короткого - 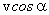 . Вдоль длинного борта шар пройдет расстояние 2b, а вдоль короткого - 2а-с. Поскольку составляющие скорости вдоль длинного и короткого бортов по величине не меняются, можно записать
. Вдоль длинного борта шар пройдет расстояние 2b, а вдоль короткого - 2а-с. Поскольку составляющие скорости вдоль длинного и короткого бортов по величине не меняются, можно записать 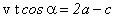 ,
, 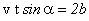 ,
,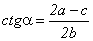 .
.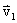 , а второго -
, а второго - 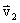 . Координаты первого тела будут изменяться со временем по закону
. Координаты первого тела будут изменяться со временем по закону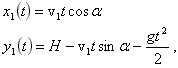
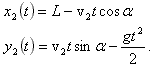
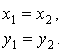
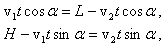
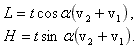
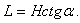
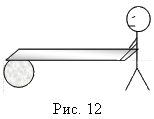 Доска при этом горизонтальна. Затем мальчик двигает доску вперед, вследствие чего цилиндр катится без скольжения по горизонтальной плоскости, отсутствует также скольжение доски по цилиндру. Какой путь должен пройти мальчик, чтобы достичь цилиндра, если длина доски равна L?
Доска при этом горизонтальна. Затем мальчик двигает доску вперед, вследствие чего цилиндр катится без скольжения по горизонтальной плоскости, отсутствует также скольжение доски по цилиндру. Какой путь должен пройти мальчик, чтобы достичь цилиндра, если длина доски равна L? . Найдите начальную скорость
. Найдите начальную скорость 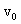 и время движения.
и время движения.