|
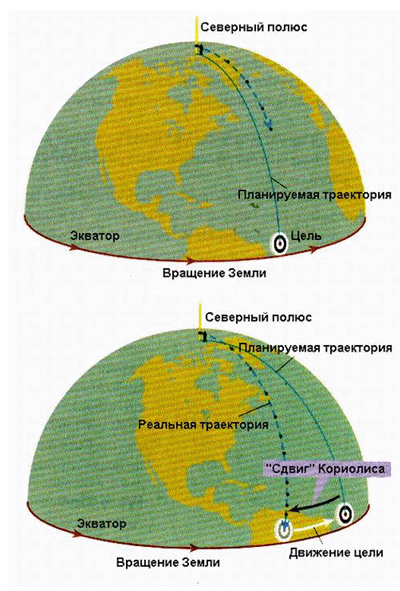
При движении тела вдоль поверхности Земли результат действия силы Кориолиса будет максимальным при движении по меридиану. При этом тело отклоняется вправо при движении с севера на юг и влево при движении с юга на север. Это обусловлено следующими причинами: первая – вращение Земли на восток, и вторая – зависимость от географической широты тангенциальной скорости точки на поверхности Земли (эта скорость равна нулю на полюсах и достигает своего максимального значения на экваторе). Таким образом, при выстреле пушки на север из любой точки на экваторе, снаряд падает восточнее своего первоначально заданного направления. Это отклонение объясняется тем фактом, что на экваторе снаряд двигается к востоку быстрее, чем в любой точке севернее. Аналогично, если стрелять со стороны северного полюса, то снаряд должен падать правее по отношению к своей прицельной точке, так как в этом случае за время полета цель успевает переместиться к востоку. Аналогичные смещения происходят при любом выстреле, если только первоначальная скорость снаряда имеет ненулевую проекцию на направление север – юг. Материалы взяты с астрономического сайта «Галактика» |
Рис. 5.7 |
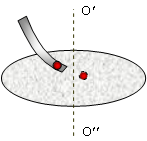
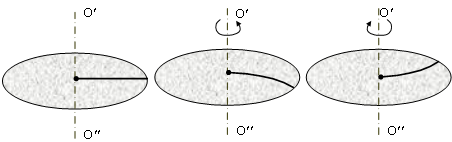
При движении тела относительно вращающейся системы координат кроме центробежной силы инерции необходимо ввести еще одну силу, которая называется силой Кориолиса. Рассмотрим движения шарика относительно вращающейся платформы (рис. 5.7). Пусть шарик скатывается на платформу. Если платформа неподвижна, то шарик движется вдоль платформы по прямой линии. При вращении платформы траектория шарика становится криволинейной. Отклонение траектории от прямолинейной происходит в сторону, противоположную вращению платформы (рис. 5.8).
В неинерциальной системе отсчета шарик движется по криволинейной траектории. Это означает, что существует сила, перпендикулярная скорости шарика относительно платформы. Увеличение угловой скорости приводит к увеличению кривизны траектории и, следовательно, к увеличению силы. При изменении направления вращения искривление траектории происходит в обратную сторону. Таким образом, в неинерциальной системе отсчета помимо центробежной силы инерции действует еще дополнительная сила – сила Кориолиса, которая зависит от скорости тела, величины угловой скорости и направления вращения.
В инерциальной системе отсчета силы, действующие в направлении, перпендикулярном скорости, равны нулю (силами трения пренебрегаем), поэтому а = 0, и движение шарика происходит равномерно и прямолинейно.
Действие сил Кориолиса является одной из причин подмывания берегов рек. Например, при течении с севера на юг в северном полушарии происходит подмывание правого (западного) берега. При течении с юга на север также подмывается правый берег, но теперь уже восточный. Ветры, дующие от тропиков к экватору, отклоняются к западу из-за действия сил Кориолиса.
В заключение отметим, что выбор системы отсчета зависит от конкретных условий. Задача решается в той системе, в которой решение проще.