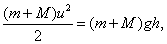Решение

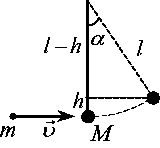Угол отклонения нити можно найти геометрически. Достаточно выразить любую из тригонометрических функций угла 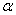. Например: 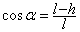. Чтобы выразить высоту подъёма шара, проще всего использовать закон сохранения энергии. Сопротивлением воздуха пренебрегаем, поэтому полная механическая энергия в нижнем и в верхнем состоянии одинакова. Считаем потенциальную энергию в нижнем положении нулевой, в верхнем положении шар останавливается – поэтому кинетическая энергия в верхней точке обращается в ноль. Таким образом, начальная кинетическая энергия полностью переходит в потенциальную:

где 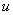 – скорость шара с пулей в нижнем положении. Шар приобретает скорость после попадания пули. Прежде чем записывать законы сохранения для этого случая, обратим внимание на то, что пуля останавливается благодаря действию на неё сил сопротивления. Нам неизвестна величина этих сил, решить задачу исходя из законов Ньютона невозможно. Законы сохранения позволяют решить задачу просто и быстро. Поскольку действуют силы сопротивления, то использовать закон сохранения энергии нельзя. Внешние силы на систему во время торможения пули в шаре скомпенсированы – сила тяжести равна силе натяжения нити. До момента попадания пули в шар импульс был только у пули – 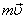. После попадания импульс равен 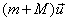. По закону сохранения импульса должно выполняться уравнение:

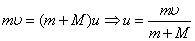Тогда

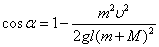Подставим числовые значения:

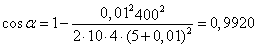По значению косинуса угла можно найти сам угол .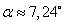

Ответ: угол отклонения нити равен 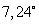.