Два мотоциклиста выезжают одновременно из двух пунктов навстречу друг другу. Один из них спускается равноускоренно с горы, имея начальную скорость 36 км/ч и ускорение 2 м/с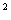 . Другой равнозамедленно поднимается в гору с начальной скоростью 72 км/ч и с тем же по модулю ускорением. Первоначальное расстояние между мотоциклистами равно 300 м. Через какое время они встретятся? Чему равны скорости мотоциклов в этот момент времени?
. Другой равнозамедленно поднимается в гору с начальной скоростью 72 км/ч и с тем же по модулю ускорением. Первоначальное расстояние между мотоциклистами равно 300 м. Через какое время они встретятся? Чему равны скорости мотоциклов в этот момент времени?
Систему отсчёта связываем с землёй. Поскольку движение в данной задаче происходит только вдоль одной прямой, то достаточно одной координатной оси. Направляем её вдоль склона горы вверх. Общий вид уравнения движения для обоих мотоциклистов имеют вид:
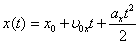 .
.Для мотоциклиста, поднимающегося в гору, начальная координата равна нулю, проекция начальной скорости на ось 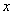 положительна, проекция ускорения отрицательна. Для мотоциклиста, спускающегося вниз по склону, начальная координата будет равна
положительна, проекция ускорения отрицательна. Для мотоциклиста, спускающегося вниз по склону, начальная координата будет равна 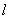 , проекция начальной скорости на ось
, проекция начальной скорости на ось 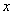 будет отрицательной, вместе с этим отрицательной будет проекция и ускорения. Часто совершают ошибку, считая, что ускорение отрицательно в случае равнозамедленного движения, а для равноускоренного движения проекция ускорения положительна. Знак проекции вектора на ось определяется взаимным расположением вектора и оси координат.
будет отрицательной, вместе с этим отрицательной будет проекция и ускорения. Часто совершают ошибку, считая, что ускорение отрицательно в случае равнозамедленного движения, а для равноускоренного движения проекция ускорения положительна. Знак проекции вектора на ось определяется взаимным расположением вектора и оси координат.
Составим уравнения движения:
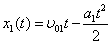
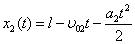 .
.В момент встречи координаты мотоциклистов равны:
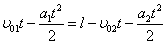 .
.Ускорения мотоциклистов одинаковы, поэтому слагаемые, содержащие квадрат времени, в обеих частях уравнения уничтожаются:
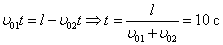 .
.Чтобы найти скорости мотоциклистов, составим вначале уравнения зависимости проекций скоростей от времени:
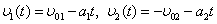 .
.Подставим в эти уравнения найденное время и значения начальных скоростей и ускорений, заданных по условию:
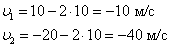 .
.Значения проекций скоростей отрицательны – это значит, что в момент встречи оба вектора направлены в сторону, противоположную оси 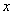 .
.
Ответ: 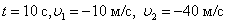 .
.