Рекуррентные вычисления – это последовательность вычислений, при которой значение самого последнего члена получаемой последовательности зависит от одного или нескольких предыдущих. В качестве примеров можно указать итерации, вычисления по рекуррентным формулам, метод прогонки, организацию решения нестационарных и граничных задач. Рекуррентные вычисления составляют определённую проблему для параллельного компьютера.

Рассмотрим для первоначального ознакомления со способами построения и анализа параллельных методов задачу нахождения частных сумм последовательности числовых значений

`SUM_k=sum_(k=1)^n` , `1<=k<=n`

(1.1)

где  `n` – количество суммируемых значений.

В последовательном алгоритме частные суммы можно вычислить весьма просто из рекуррентного соотношения

`SUM_k=SUM_(k-1)+x_k;k=bar(1,n);SUM_0=0`.

(1.2)

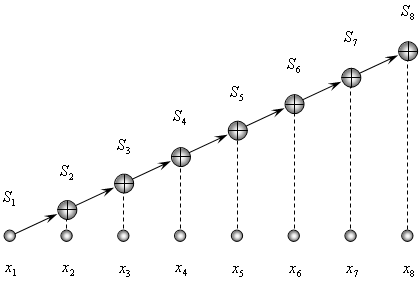
Рис.1.1. Схема последовательного алгоритма вычисления частных сумм

Соотношение между способом хранения данных, арифметическими операциями и временем можно изобразить на диаграмме маршрутизации (Рис.1.1). Имеющаяся последовательность вычислений перемещается снизу вверх. Операции, которые могут выполняться параллельно, показаны на одном и том же вертикальном уровне. Ясно, что на каждом временном уровне может выполняться только одна операция (степень параллелизма равна единице) и мы говорим, что алгоритм последовательных сумм имеет  `n-1` сложение со степенью параллелизма 1.

Данный алгоритм суммирования допускает только строго последовательное исполнение и не может быть распараллелен.