Скалярное произведение двух векторов размерности `n` определяется по формуле:

`vecx^T vecy = sum_(i=1)^n x_i y_i`

(2.1)

и требует `n` умножений и `n-1` сложений. Для простоты время выполнения последовательного алгоритма на обычном компьютере может быть представлено как

`T_1 = t_c*n` ,

где - `t_c= max (t_(a d),t_(m u))` время выполнения одной скалярной операции «умножение-сложение».

Следуя описанной во введении общей методологии построения алгоритмов для параллельной вычислений,

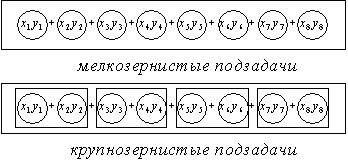
1. разобьем задачу на более мелкие подзадачи, а именно мелкозернистая подзадача `i` запоминает компоненты `x_i,y_i` , и вычисляет произведение `x_i*y_i` ;
2. коммуникации между подзадачами устанавливаются таким образом, чтобы обеспечить суммирование полученных произведений;
3. укрупнение подзадач производится путем объединения `n//p` (`p` - предполагаемое число процессоров) мелкозернистых подзадач с сохранением коммуникаций между крупнозернистыми подзадачами;
4. каждая укрупненная подзадача назначается на выполнение одному процессору `p` -процессорной вычислительной системе.

На рис. 2.1 представлены описанные выше этапы построения параллельной вычислительной процедуры.

Рис.2.1. Параллельный алгоритм вычисления скалярного произведения