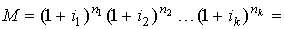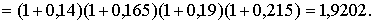При начислении сложных процентов происходит их капитализация (проценты присоединяются к той сумме, которая служила базой для их начисления). Таким образом, база начисления сложных процентов увеличивается от одного расчетного периода к другому. В этом случае говорят, что используется сложная процентная ставка.

Формула наращения по сложным процентам имеет вид

,

где

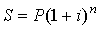P – исходная сумма;

S – наращенная сумма;

i – годовая ставка сложных процентов;

n – срок операции в годах;

(1 + i)ⁿ – множитель наращения сложных процентов.

 

Проценты за весь срок операции определяют по формуле

.

 

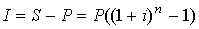Пример 5.

Кредит в сумме 100 тыс. руб. выдан на 2 года под сложную процентную ставку 30 % годовых. Найдите наращенную сумму и сумму процентов.

Решение. P = 100 000; i = 0,3; n = 2. По формуле сложных процентов получаем наращенную сумму

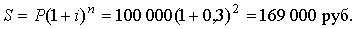Сумма начисленных процентов

♦

 

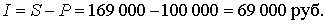Если срок операции n измеряется дробным числом лет, то можно использовать комбинированную схему начисления процентов, когда на целое число лет начисляются сложные проценты, а на дробную часть срока – простые. В этом случае

,

где

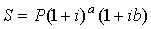a + b = n; a – целое число лет; b – дробная часть года.

 

Пример 6.

Вклад в сумме 40 000 руб. внесен в банк под 10 % годовых с ежегодной капитализацией. Определите сумму вклада через 3,5 года, применяя комбинированную схему начисления процентов.

Решение. P = 40 000; i = 0,1; n = 3,5 (= 3+0,5). Применяем формулу комбинированных процентов:

♦

 

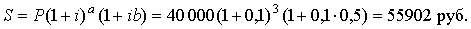При переменной ставке сложных процентов наращенная сумма вычисляется по формуле

,

где

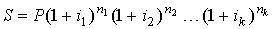n₁, n₂,…, n_k – интервалы времени, следующие друг за другом, (n₁ + … + n_k = n);

i₁, i₂,…, i_k – соответствующие им ставки процентов.

 

Пример 7.

Фирма взяла в банке кредит 6 млн руб. сроком на 4 года. Согласно договору за первый год процентная ставка составляла 14 % годовых и с учетом инфляции каждый последующий год повышалась на 2,5 %. Определите коэффициент наращения, наращенную сумму и доход банка при ежегодной капитализации процентов.

Решение. P = 6. Срок кредита n = 4 года разбит на 4 периода (k = 4):

1) i₁ = 0,14; n₁ = 1;

2) i₂ = 0,165; n₂ = 1;

3) i₃ = 0,19; n₃ = 1;

4) i₄ = 0,215; n₄ = 1.

Находим множитель наращения

Наращенная сумма

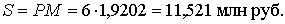Доход банка

♦

 

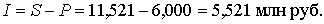Если сложные проценты начисляются несколько раз в год (например, ежеквартально или ежемесячно), используют формулу

,

где

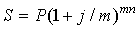j – номинальная ставка процентов (годовая ставка сложных процентов);

m – количество периодов начисления процентов в год;

j/m – ставка за один период;

mn – общее количество периодов за весь срок;

(1 + j/m)^mn – множитель наращения при m-разовом начислении сложных процентов.

 

Пример 8.

Ссуда в размере 10 тыс. руб. выдана на 2,5 года под 12 % годовых. Определите наращенную сумму ссуды при ежеквартальной капитализации процентов.

Решение. P = 10 000; j = 0,12; n = 2,5; m = 4. Период начисления процентов – квартал; ставка за период j/m = 0,03; всего периодов начисления mn = 10. Вычисляем наращенную сумму:

♦
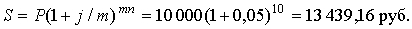