Своеобразным инвестиционным проектом является аренда оборудования. Арендатору необходимо решить, что выгоднее: купить оборудование или арендовать его, а арендодателю важно правильно определить размер арендной платы и финансовую эффективность от аренды оборудования.

 

Пусть оборудование стоимостью P сдается в аренду на n лет, остаточная стоимость оборудования к концу срока аренды равна S. Тогда «потери» арендодателя равны:

D = P – S/(1 + i)ⁿ,

где i – ставка дисконтирования.

 

Современная стоимость потока арендных платежей должна составлять сумму «потерь» арендодателя. Из этого условия определяется размер арендной платы. Так, если арендные платежи выплачиваются один раз в конце года, получаем:

,

где

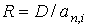R – размер платы за аренду оборудования;

a_n,i – коэффициент приведения постоянной годовой ренты.

 

Чтобы определить эффективность сдачи оборудования в аренду при заданных арендных платежах, требуется решить обратную задачу: найти ставку дисконтирования, при которой современная величина потока арендных платежей равна сумме «потерь» арендодателя. В Microsoft Excel эту задачу можно решить с помощью команды Подбор параметра в меню Сервис.

 

Пример 49.

Оборудование стоимостью 1 млн руб. сдано в аренду на 4 года. Остаточная стоимость на момент окончания аренды оценивается в 400 тыс. руб. Требуемая доходность от вложений в оборудование определена на уровне 15 % годовых. Определите размер арендной платы, обеспечивающей заданную доходность, при условии, что арендные платежи вносятся один раз в начале года.

Решение. P = 1 000 000; S = 400 000; n = 4; i = 0,15. Арендные платежи можно рассматривать как постоянную годовую ренту пренумерандо, ее современная величина равна Ra_n,i(1 + i) . Современная стоимость потока арендных платежей должна составлять сумму «потерь» арендодателя:

♦
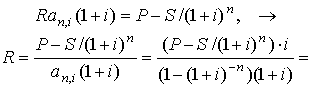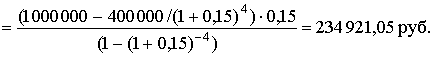