Предполагается, что рентные платежи поступают p раз в год в сумме R за год, а проценты на них начисляются непрерывно (m → ∞) с постоянной силой роста δ. Формулы расчета обобщающих характеристик p-срочной ренты с непрерывным начислением процентов имеют вид

,

,

где

,

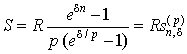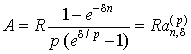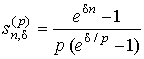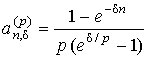– коэффициенты наращения и приведения соответствующей ренты.

 

Взаимосвязь между наращенной суммой и современной величиной определяется соотношениями:

,

,

где e^δn – множитель наращения непрерывных процентов.

 

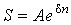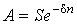Пример 27.

 Пусть платежи поступают в конце года равными суммами в размере 5 тыс. руб., проценты начисляются непрерывно с силой роста 20 % годовых. Найдите современную величину и наращенную сумму ренты при условии, что она выплачивается 10 лет.

Решение. Имеем обычную постоянную годовую ренту с непрерывным начислением процентов: R = 5 000; δ = 0,2; n = 10. Ее современная величина равна

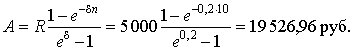Наращенную сумму найдем через уравнение взаимосвязи S и A:

♦
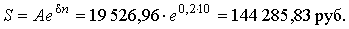