Обычная годовая рента с начислением процентов m раз в год предусматривает начисление сложных процентов более одного раза в год по ставке j/m, где j – номинальная ставка процентов; m – количество периодов начисления процентов в год. Платежи поступают один раз в конце года в сумме R в течение n лет, mn – общее количество периодов начисления процентов. В этом случае

,

,

где

 

,

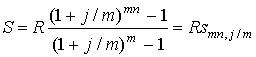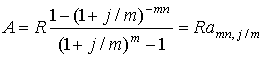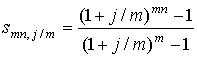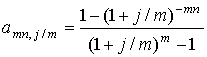– коэффициенты наращения и приведения соответствующей ренты.

 

Взаимосвязь между наращенной суммой и современной величиной определяется соотношениями:

,

,

где (1 + j/m)^mn – множитель наращения при m-разовом начислении сложных процентов.

 

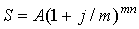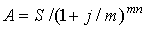Пример 21.

Страховая компания заключила договор с фирмой на 3 года, согласно которому поступающие в конце каждого года взносы в размере 5 млн руб. она помещает в банк под 15 % годовых с поквартальным начислением процентов. Определите итоговую сумму, полученную страховой компанией. Как изменится результат при сроке договора 3,5 года?

Решение. Имеем обычную постоянную годовую ренту с начислением процентов m раз в год: R = 5 000 000; j = 0,15; m = 4; n = 3. Ее наращенная сумма будет представлять собой итоговую сумму договора:

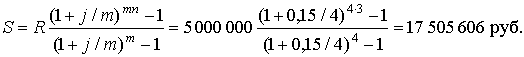При сроке договора 3,5 года срок ренты остается равным 3 годам. Итоговая сумма договора будет равна наращенной сумме ренты за 3 года плюс начисленные на нее проценты за оставшиеся полгода. Используя формулу m-разового начисления сложных процентов, получаем

♦
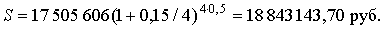