Лабораторная работа 9. Теплоемкость газа Бозе–частиц.

 

Цель работы

Рассмотреть пример использования системы Maple к решению задачи о вычислении теплоемкости системы Бозе–частиц.

 

Объект исследования

            Рассмотрим систему  бозе частиц с ненулевой массой  (например He⁴) при температурах близких к абсолютному нулю, когда возникает явление сверхтекучести. Предположим также, что система занимает объем  и находится в равновесии с внешней средой при температуре . Среднее число частиц с энергией в интервале от  определяется, как известно [2], распределением Бозе–Эйнштейна:

                                                                                                                             (1)

где   в нашем случае имеет вид

,                                                                                                                  (2)

где  ( – постоянная Больцмана) статистическая температура. Величина  химический потенциал, и его зависимость от  определяется условием нормировки:

.                                                                                                 (3)

Для Бозе–газа можно показать, что  и  для . Из уравнения (3) следует, что при  существует критическая температура :

                                                                                                                            (4)

Используя зета – функцию Римана

,                                                                                                                         (5)

выражение (4) переписывается в виде

.                                                                                                                        (6)

Для  химический потенциал  и условие нормировки принимает вид

,                                                                                                                        (7)

где  – число частиц в основном состоянии с энергией . Состояние, в котором частицы ведут себя особым образом, называемым сверхтекучим. Таким образом, химический потенциал как функция температуры имеет две различные области  при  и определяется из уравнения (3) при .

Наша задача состоит в том, чтобы найти температурную зависимость теплоемкости при постоянном объёме такой системы. По определению

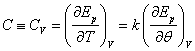,                                                                                                                    (8)

где  есть энергия, приходящаяся на одну частицу, и определяется из уравнения

.                                                                                                    (9)

Введем функцию

,                                                                                                    (10)

которую называют интегралом Бозе–Эйнштейна. Нетрудно видеть, что .