В этом параграфе мы покажем, что линейное неоднородное уравнение с постоянными коэффициентами

,

(2.5.12)

где и – многочлены, имеет частное решение вида

,

(2.5.13)

где и – многочлены, степени которых не выше наибольшей из степеней многочленов , , а – число равных корней характеристического многочлена

(2.5.14)

Напомним ранее полученную формулу характеристического многочлена

(2.5.15)

Выгодно в правой части уравнения (2.5.12) тригонометрические функции выразить через показательные по формулам Эйлера:

,

Тогда уравнение(2.5.12) можно записать в виде

,

(2.5.12а)

где – многочлен, степень которого равна наибольшей из степеней многочленов , .

Теорема о суперпозиции. Если – решение уравнения

,

(2.5.13а)

а – решение уравнения

,

(2.5.13б)

то функция есть решение уравнения

.

(2.5.13)

Дано:

, .

(2.5.13в)

Тогда (по свойству линейности и формулам (2.5.11в)) ,

что и доказывает эту теорему.

Теорема о суперпозиции позволяет вопрос о решении уравнения (2.5.13) свести к решению двух уравнений

,

(2.5.14)

.

(2.5.14а)

Но это уравнения одного типа. Достаточно решить одно из них, чтобы переходом к сопряженным величинам получить решение другого.

Рассмотрим первый случай, когда не является корнем характеристического многочлена, , .

Тогда при имеем

.

(2.5.15а)

Это тождество показывает, что при подстановке в левую часть (2.5.14) функции получается произведение того же показательного множителя на многочлен степени (ибо коэффициент при в правой части (2.5.15а) отличен от нуля). Следовательно,

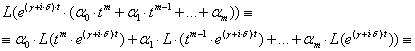
(по (2.5.15) при )

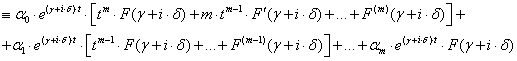(2.5.16)

Можно поэтому подобрать коэффициенты так, чтобы правая часть

(2.5.16) совпала с правой частью (2.5.14), т. е.

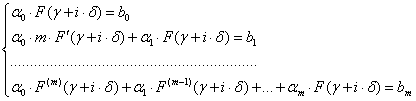
Но эта система легко решается, ибо по условию (2.5.15) :

, ,

Пусть теперь характеристический многочлен (2.5.15а) имеет корней, равных . Тогда

, ,…, ,

(2.5.17)

и (2.5.15а) принимает вид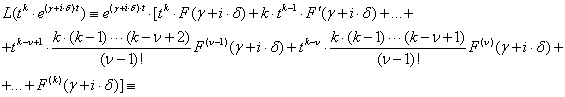

(по условию (2.5.17))

– степень многочлена понизилась на . Следовательно, чтобы , надо многочлен брать степени, большей степени многочлена на единиц, причем число коэффициентов многочлена должно совпадать с числом коэффициентов многочлена , т. е. если , то частное решение неоднородного уравнения (5.14) можно искать в виде

.

(5.18)

Остальное делается аналогично случаю .