Частное решение неоднородной линейной дифференциальной системы можно найти методом вариации произвольных постоянных, с которыми мы познакомились при решении линейного однородного уравнения первого порядка.

Рассмотрим однородную систему, соответствующую неоднородной системе (2.5.1)

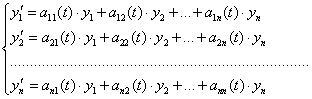(2.5.3)

или в краткой векторно-матричной записи

,

(2.5.3а)

где использованы обозначения (2.5.2) или еще в более краткой записи

,

(2.5.3б)

где

.

(2.5.3в)

Оказывается, что фундаментальная система

, ,…,

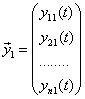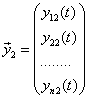(2.5.4)

решений линейной однородной системы

,

(2.5.4а)

(2.5.5)

соответствующей неоднородной системе (2.5.1), достаточна для получения общего решения неоднородной системы (2.5.1б).

Возьмем общее решение (2.5.3а) линейной однородной системы

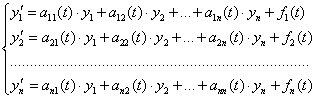(2.5.5)

и заменим входящие в него произвольные постоянные на такие дифференцируемые функции , чтобы

(2.5.6а)

стало решением неоднородной системы (2.5.1а).

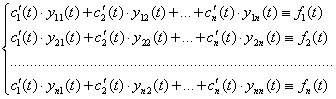(2.5.6б)

Если эти равенства рассматривать как алгебраическую линейную систему с неизвестными , то определителем этой системы будет –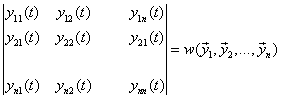

вронскиан для базисной, т.е. линейно независимой системы решений (2.5.3) линейной однородной системы (2.5.4), который не обращается в нуль на промежутке . Следовательно, алгебраическая система (2.5.6б) имеет единственное решение

, ,…, ,

(2.5.7)

где функции непрерывны на . Переходя в (2.5.7) к первообразным, найдем

, ,…, ,

(2.5.7а)

Они подобраны так, что для них выполняется (2.5.6б), а функция

(2.5.5а)

есть решение неоднородной системы (2.5.1а).