1.2. Изоклины. Составление дифференциального уравнения семейства кривых

Изоклины. [1, с. 11], [2, п. 1.1, 1.2], [3, с. 9 – 14].

1. Степанов В.В. Курс дифференциальных уравнений. - М.: Едиториал УРСС. 2004. - 472 с.

2. Малютина А.Н. Лекции по дифференциальным уравнениям. ТГУ, 2009.

3. Эльсгольц Л. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1966.

Геометрическое место точек плоскости , в которых наклон касательных к решениям уравнения один и тот же, называется изоклиной. Следовательно, уравнение изоклины имеет вид , где постоянная равная тангенсу угла наклона касательной к оси абсцисс.

Чтобы приближенно построить решения уравнения можно начертить достаточное число изоклин, а затем провести решения, т.е. кривые, которые в точках пересечения с изоклинами

имеют касательные с угловыми коэффициентами

Пример 3.

С помощью изоклин начертить приближенно решения уравнения

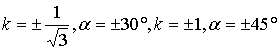Решение. Уравнение изоклин или , т. е. для различных уравнения парабол. Начертим изоклины для , что соответствует , черточками изобразим отрезки касательных к решениям, пересекающим изоклины, и начертим решения исходного уравнения.

РИС.

Задачи [4]. № 1 – 16.

4. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. М.: Наука, 1973.

Составление дифференциальных уравнений семейства кривых.

Чтобы построить дифференциальное уравнение, которому удовлетворяют кривые семейства (1) надо продифференцировать это равенство раз, считая функцией от , а затем из полученных уравнений и уравнения (1) исключить постоянные .

Пример 4.

Составить дифференциальное уравнение семейства кривых

Решение. Так как это уравнение содержит лишь одну произвольную постоянную, то продифференцируем его один раз, будем иметь . Теперь из системы ,, исключим произвольную постоянную , для этого прологарифмируем первое неравенство, будем иметь , т.е. , заменяя в первом равенстве на , и на получим дифференциальное уравнение данного семейства кривых, уравнение вида

Пример 5.

Составить дифференциальное уравнение семейства кривых

(1.2.1)

Решение. Так как уравнение семейства содержит два параметра, дифференцируем его два раза, считая :

(1.2.2)

(1.2.3)

Исключаем . Из уравнения (1.3) имеем ; подставляя это в (1.2.2), получим

(1.2.4)

Исключаем . Из уравнения (1.2.3) имеем 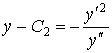; подставляя это в (1.2.4), получим после упрощений дифференциальное уравнение

Контрольные вопросы и задачи

1. Как возникают дифференциальные уравнения при математическом моделировании реальных процессов? (привести примеры). Как составить дифференциальное уравнение заданного однопараметрического семейства кривых?

2. Какое уравнение называется обыкновенным дифференциальным уравнением? Что такое порядок дифференциального уравнения; степень дифференциального уравнения? Всякое ли дифференциальное уравнение имеет степень?

Задачи [4] № 17 – 36.