1.6. Уравнения в полных дифференциалах. Интегрирующий множитель
[1, гл. II, с. 94], [2, п. 2.7], [3, с. 32 – 37]
1. Уравнение
(1.6.1) |
называется уравнением в полных дифференциалах, если левая часть является полным дифференциалом некоторой функции ![]() . Это имеет место, если
. Это имеет место, если
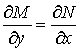 .
.
Чтобы решить уравнение (6.1), надо найти функцию ![]() , от которой полый дифференциал
, от которой полый дифференциал
![]()
равен левой части уравнения (6.1). Тогда общее решение уравнения (1.5.1) можно написать в виде ![]() , где
, где ![]() - произвольная постоянная.
- произвольная постоянная.
Пример 1.
Решить уравнение
(1.6.2) |
Решение. Так как
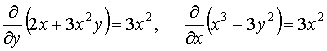 ,
,
то уравнение (1.6.2) является в полных дифференциалах. Найдем функцию ![]() , полый дифференциал которой
, полый дифференциал которой
![]()
был бы равен левой части уравнения (6.2), т.е. такую функцию ![]() ,что
,что
(1.6.3) |
Интегрируем по ![]() первое из уравнений (1.6.3), считая
первое из уравнений (1.6.3), считая ![]() постоянным; при этом вместо постоянной интегрирования надо поставить
постоянным; при этом вместо постоянной интегрирования надо поставить ![]() - неизвестную функцию от
- неизвестную функцию от ![]()
![]()
Подставляя это выражение для ![]() во второе из уравнений (6.3) найдем
во второе из уравнений (6.3) найдем ![]() :
:
![]() .
.
Следовательно, можно взять ![]() и общее решение уравнения (1.6.2) будет иметь вид
и общее решение уравнения (1.6.2) будет иметь вид
![]() .
.