К однородным уравнениям можно привести некоторые дифференциальные уравнения с помощью замены , где неизвестно и определяется из условия, что замена обращает исходное уравнение в однородное.

Пример 1.

Решить уравнение

Решение. Уравнения вида 10) при замене получим . Чтобы полученное уравнение было однородным, нужно чтобы суммы показателей степеней сомножителей совали для всех слагаемых. т.е , и исходное уравнение при замене имеет вид или т. е. вид однородного уравнения 11.

Задачи [4]. №121-129.

4. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. М.: Наука, 1973.

1.5. Линейные уравнения первого порядка

[1, с. 34], [2, п. 2.4], [3, с. 27 – 31]

1. Степанов В.В. Курс дифференциальных уравнений. - М.: Едиториал УРСС. 2004. - 472 с.

2. Малютина А.Н. Лекции по дифференциальным уравнениям. ТГУ, 2009.

3. Эльсгольц Л. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1966.

1. Линейным дифференциальным уравнением первого порядка называется уравнение линейное относительно неизвестной функции и ее производной, т. е. уравнение вида

(1.5.1)

где функции и непрерывны.

Чтобы его решить надо сначала решить уравнение

(1.5.2)

Это уравнение называется линейным однородным, соответствующим (1.5.1).(Это делается путем разделения переменных см. п. 1.2) и в общем решении последнего заменить произвольную постоянную на неизвестную функцию . Затем выражение, полученное для , подставить в уравнение (1.4.1) и найти функцию .

2. Некоторые уравнения становятся линейными, если поменять местами искомую функцию и независимое переменное. Например, уравнение , в котором является функцией от , - нелинейное. Запишем его в дифференциалах

Так как в это уравнение и входят линейно, то уравнение будет линейным, если считать искомой функцией, а - независимым переменным. Это уравнение может быть записано в виде

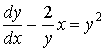и решается аналогично уравнению (1.5.1).

3. [2, п. 2.5] Уравнение вида

(1.5.3)

называется уравнением Бернулли. Чтобы его решить надо обе его части разделить на и сделать замену . После замены получается линейное уравнение, которое можно решить изложенным выше способом.

4. [2, п. 2.6]. Уравнение вида

(1.5.4)

в котором правая часть есть квадратичная функция от искомой функции у, называется уравнением Риккати.

Оно не решается в общем случае. Если же известно одно частное решение , то заменой уравнение Риккати сводится к уравнению Бернулли и таким образом может быть решено в квадратурах. (напомним: Решение дифференциального уравнения в квадратурах — нахождение решения в виде комбинации элементарных функций и интегралов от них)

Будем полагать, что P(x), Q(x), R(x) определены и непрерывны в интервале (a,b). Тогда через всякую точку полосы проходит одна и только одна интегральная кривая уравнения Риккати. Однако в отличие от линейного уравнения для уравнения Риккати эта интегральная прямая в общем случае определена не во всем интервале (a,b), а лишь в некоторой окрестности начального значения независимой переменной.

Всякая интегральная прямая уравнения Риккати представляет собой график частного решения этого уравнения, так что особых решения уравнение Риккати не имеет.

Интегрируется в квадратурах уравнение Риккати только в исключительных случаях.

Если известно частное решение уравнения Риккати, то подстановка , где z-новая неизвестная функция, приводит это уравнение к линейному.

Уравнение Риккати вида:

, где А, В, С- постоянные числа, причем имеет частное решение , где а – некоторое постоянное число, определяемое подстановкой в уравнение. Так же это уравнение является обобщенным однородным уравнением, в котором k=-1 и подстановкой приводится к уравнению с разделяющимися переменными.

Уравнения Риккати вида:

или

подстановкой приводится к уравнению с разделяющимися переменными

и всегда интегрируется в элементарных функциях.