Рассмотрим работу цикла со счетчиком на примере следующей задачи.

ЗАДАЧА 1.4. Пользователь вводит последовательность из 10 чисел. Требуется определить максимальное значение.

В задаче четко указано, что нужно рассмотреть 10 чисел, значит, до начала циклических действий мы можем сказать, сколько раз будет выполняться тело цикла. В таком случае эффективнее всего использовать цикл с параметром.

Для решения задачи воспользуемся свойством дискретности алгоритма. Определим первоначальное значение переменной max равной первому введенному числу. Будем последовательно сравнивать значение переменной max со всеми последующими числами. В такой интерпретации алгоритма мы каждый раз решаем уже известную для нас задачу – ЗАДАЧУ 1.3. (поиск максимального из двух значений). В роли первого участника алгоритма выступает max, а рассматриваемое в данный момент число – в роли второго участника алгоритма.

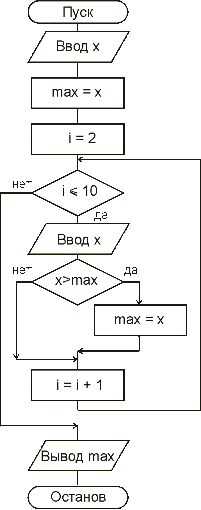
В качестве параметра цикла будем использовать переменную i. Ее начальное значение будет равно 2 (первое из введенных чисел мы сразу определи в переменную max). Будем значение параметра цикла наращивать на единицу всякий раз после рассмотрения очередного числа. Когда все 10 чисел будут рассмотрены, закончим циклические действия. На ‎Рис. 1.25 представлены блок-схемы этого алгоритма с использованием специальной геометрической фигуры для цикла с параметром и без нее.

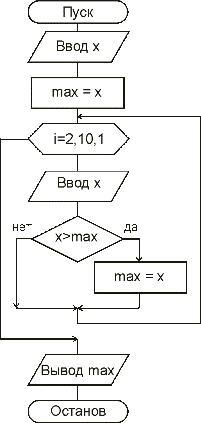Рис. 1.25.  Блок-схема решения задачи 1.4.