Исследование

Шаг 1. Замена переменных и предварительный анализ данных

Переменная 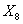измерена в номинальной шкале и значит непосредственное включение её в регрессионное уравнение будет некорректным. Оставить переменную без изменений фактически означало бы, что мы допускаем арифметическую операцию сложения материалов, например, 1 (кирпич) + 3 (шлакоблок) = 4 (дерево), что, конечно, не имеет смысла. Заменим её набором из четырёх фиктивных переменных, принимающих только два значения – 0 или 1:

– переменная равна 1, если стены дома кирпичные, иначе 0;

– переменная, равна 1, если стены дома панельные, иначе 0;

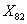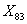– переменная, равна 1, если материал стен – шлакоблок, иначе 0;

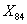– переменная, равна 1, если стены дома изготовлены из дерева, иначе 0.

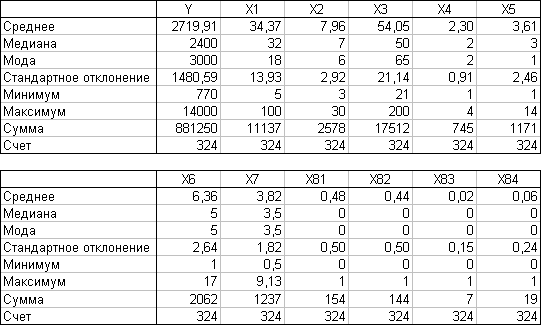
Для знакомства с имеющимися данными и проверки отсутствия в них явно некорректных значений построим описательную статистику (рис. 25), корреляционную матрицу (рис. 26) и гистограмму распределения цен (рис. 27).

Анализ данных описательной статистики (см. рис. 25) позволяет сделать следующие выводы:

1. Выборка содержит 324 наблюдения.
2. В выборке представлены данные об одно-, двух-, трёх- и четырёхкомнатных квартирах (см. минимум и максимум ).
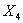3. Большинство наблюдений выборки относится к двухкомнатным квартирам (см. моду );
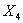4. В основном квартиры находятся в пятиэтажных домах, и большинство расположено на первом этаже (см. моду 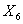и ).
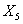5. Наиболее популярный материал для постройки дома – кирпич и бетон; дерево и шлакоблок используются очень редко (см. суммы соответствующих переменных).

Описательная статистика не обнаружила таких явно некорректных значений, как отрицательные значения площадей, цен, этажей и расстояний, но, по крайней мере, одна квартира, принимая во внимание, что минимальный размер общей площади 20 м², имеет подозрительно малый размер жилой площади – 5 м². Возможно это ошибка, допущенная при вводе данных; поэтому не лишним будет провести дополнительный анализ и очистку исходных данных.

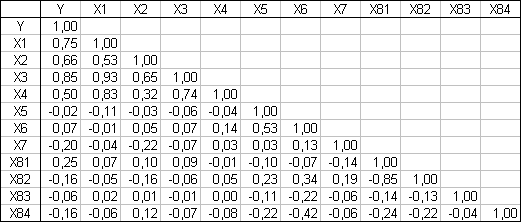
Корреляционная матрица (см. рис. 26) даёт следующую информацию о характере влияния имеющихся факторов на цену квартиры (все выводы здесь делаются только на основании данных первого столбца, т.к. анализируется влияние имеющихся факторов на стоимость квартиры):

1. Жилая площадь, площадь кухни и общая площадь квартиры оказывают сильное положительное влияние на стоимость квартиры (значения коэффициентов корреляции равны 0,75, 0,66 и 0,85 соответственно).
2. Количество комнат оказывает умеренное положительное влияние на цену (значение коэффициента корреляции равно 0,5).
3. Этаж и количество этажей в доме практически никак не связаны со стоимостью квартиры (значение коэффициентов корреляции равны −0,02 и 0,07 соответственно).
4. Удалённость от центра города оказывает слабое отрицательное влияние на стоимость квартиры (коэффициент корреляции равен −0,2).
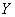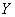5. Квартиры в кирпичных домах более привлекательны и поэтому имеют более высокую стоимость, чем в домах из других материалов (коэффициент корреляции между и положительный, между и 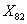, , 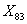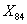– отрицательный).

В целом корреляционная матрица не выявила каких-либо серьёзных аномалий в исходных данных, т.к. почти все сделанные выводы не противоречат здравому смыслу, кроме вывода об отсутствии связи между ценой квартиры и этажом. Возможными причинами столь странного вывода являются особенность имеющихся данных или же уникальная особенность жителей города Томска. Скорее всего в регрессионном уравнении оба фактора окажутся незначимыми.

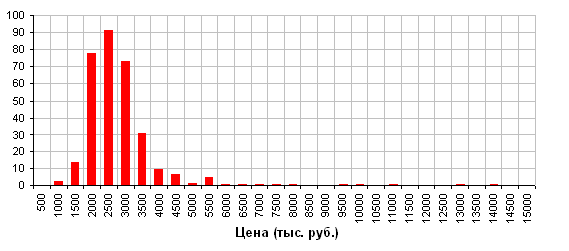
Гистограмма распределения цен на квартиры (см. рис. 27) имеет почти симметричный вид с небольшим перекосом справа. Похожий график имеет плотность случайной величины, распределённой по логарифмически нормальному закону, поэтому наряду с простой линейной моделью имеет смысл исследовать зависимость логарифма цены от имеющихся факторов – возможно, такая модель окажется лучше.