Проверим теперь предположение о нормальном распределении остатков, используя графический метод. Для этого упорядочим остатки e1,…, en в порядке возрастания

e(1)<e(2)<…<e(n).
и нанесем на плоскость точки
,
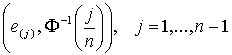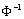где – функция, обратная к функции стандартного нормального закона. Известно, что если выборка e1,…en действительно взята из нормального распределения со средним 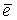и дисперсией s2, то эти точки должны оказаться вблизи прямой линии 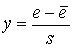. Поскольку выборочное среднее остатков 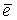= 0, “нормальные” остатки должны оказаться вблизи прямой .

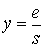Построим следующую таблицу (рис. 12): первый столбец – значение переменной j = 1,…, n, второй столбец – упорядоченные
значения остатков e(j), третий столбец – значения функции
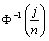для j = 1,…, n–1, последний столбец – .

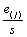1. Первый столбец легко заполнить, воспользовавшись режимом автозаполнения.

Рис. 12. Анализ остатков

 

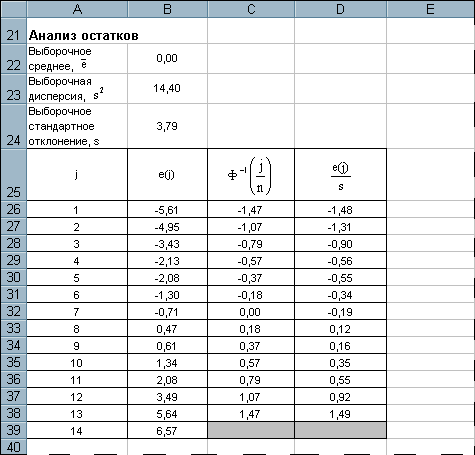
2. Чтобы заполнить второй столбец таблицы, скопируйте ячейки E3:E16, затем выделите ячейку B26 и выполните в меню Правка команду Специальная вставка. В появившемся диалоговом окне установите переключатель Вставить значения и щелкните кнопку OK. Убедитесь, что диапазон ячеек B26:B39 выделен, и щелкните кнопку Сортировка по возрастанию.

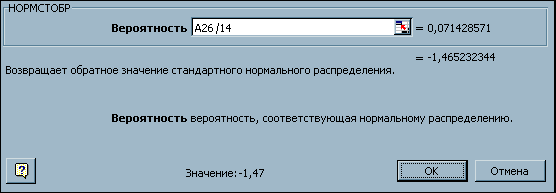
3. Для вычисления значений обратной функции 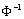стандартного нормального распределения воспользуемся встроенной функцией НОРМСТОБР (рис. 13). Для этого выделите ячейку C26, вызовите Мастер функций и из списка Статистических функций выберите НОРМСТОБР. В диалоговом окне задания аргументов функции в поле Вероятность введите формулу A26/14, как это показано на рис. 13, и щелкните кнопку OK. В результате в ячейке C26 появится формула =НОРМСТОБР(A26/14). Скопируйте ее автозаполнением в интервал ячеек C27:С38 (на одну меньше, чем значений остатков).

Рис. 13. Задание аргументов функции НОРМСТОБР

 

4. Чтобы заполнить последний столбец таблицы, введите в ячейку D26 формулу =B26/$B$24 и скопируйте ее автозаполнением в интервал D27:D38.

По данным диапазона B26:D38 строим точечную диаграмму (рис. 14). Для первого ряда данных устанавливаем цвет фона маркера Белый, для второго ряда – тип линии Обычная и тип маркера Отсутствует. Для шкалы оси Y указываем Ось X пересекает в значении –2, для оси X – Ось Y пересекает в значении –6.

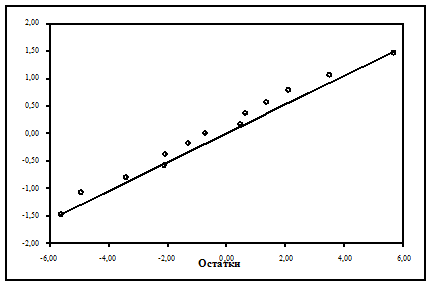
Рис. 14. График остатков: диапазон исходных данных B26:D38

 

Из полученного графика видно, что остатки достаточно хорошо ложатся на прямую. Поэтому будем считать, что предположение о нормальном распределении остатков выполнено.