При падении света на прозрачную диэлектрическую пластинку он частично преломляется, а частично отражается от обеих её поверхностей. Рассмотрим падение параллельного пучка света из вакуума или воздуха на плоскопараллельную прозрачную пластинку толщиной d (рис. 1). Угол падения (и угол отражения) равен α, а угол преломления – β. Показатель преломления вещества пластинки равен n. В точке А волна частично преломляется (луч АВ), а частично отражается (луч АС). Какая доля энергии отражается, а какая преломляется, зависит от соотношения показателей преломления сред и угла падения, для стекла (показатель преломления 1,5) при лобовом падении волны из вакуума или воздуха отражается около 4 процентов падающей энергии, а остальные 96 процентов преломляется. Преломлённая волна, в свою очередь, падает на нижнюю грань пластинки, и в точке В волна снова делится на две. То же самое происходит в точке D и т.д. В итоге от пластинки отражаются две волны (лучи 1 и 2), и также будут две преломлённые волны. Вообще говоря, будут происходить и дальнейшие отражения и преломления, но энергия и амплитуда этих последующих волн ничтожно мала.
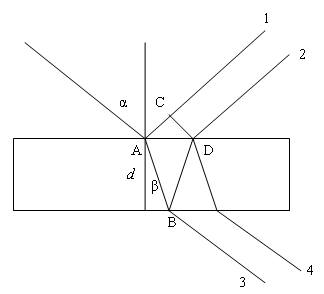 |
| Рис. 1 |
Вычислим разность хода отражённых волн 1 и 2. Поскольку пластинка плоскопараллельная, то отражается от неё параллельный пучок лучей, т.е. плоская волна. Поэтому точки С и D являются точками фронта отражённой волны, и по этой причине при дальнейшем распространении волны разность хода между волнами 1 и 2 не будет изменяться и останется такой, какой она стала раньше. Таким образом, разность хода этих волн должна быть равной разности пройденных волнами путей АВD и АС, но нужно учесть, что путь АВD волна проходит в среде с показателем преломления n, а путь АС – в воздухе с показателем преломления, практически равным единице. Таким образом, оптическая разность хода равна:
 |
Эту формулу необходимо исправить для случая, когда одна из волн отражается от среды с большим показателем преломления. В этом случае наблюдается так называемая потеря полуволны, при этом разность фаз мгновенно изменяется на величину π, а разность хода – на половину длины волны. Это имеет место и в нашем случае: волна 1 появляется как раз в результате такого отражения (граница воздух – стекло), а волна 2 появляется в результате отражения от воздуха. Таким образом, с учётом сказанного разность хода волн, отражённых от верхней и нижней граней пластинки, равна
| (1) |
она зависит от толщины пластины d, её показателя преломления n, угла падения a и длины волны света в вакууме l.
Отражённые волны когерентны и поэтому интерферируют. Если разность хода равна целому числу длин волн, то наблюдается максимум интерференции, а если полуцелому – то минимум.
Амплитуды волн, отражённых от верхней и нижней поверхностей пластинки (1 и 2), малы, но они почти не отличаются друг от друга, поэтому в отражённом свете будет наблюдаться чёткая интерференционная картина с резко выраженными минимумами и максимумами. Амплитуды волн, прошедших через пластинку (3 и 4), напротив, сильно отличаются друг от друга: энергия и амплитуда у волны 3 очень велика, а у волны 4 мала. Поэтому при интерференции этих волн интенсивность света в максимумах и минимумах будет слабо различаться, и поэтому интерференционная картина будет нечёткой.
Для монохроматического света условия максимумов и минимумов интерференции зависят от угла падения, следовательно, при его варьировании (т.е. при повороте плёнки относительно светового луча) изменяется освещённость плёнки, а при некоторых значениях этого угла, при которых выполняется условие минимума, плёнка почти не отражает падающего на неё света. На этом основано «просветление» оптики, для этого элементы оптической схемы (линзы и т.п.) покрывают тонкой плёнкой вещества такой толщины, что для случая лобового падения света при длине волны, соответствующей наиболее хорошо воспринимаемому глазом жёлтому свету, выполняется условие минимума для отражённой волны.
Если на плёнку падает белый свет, в состав которого входят волны с разной длиной волны, то условие максимумов и минимумов должно выполняться для каждой его монохроматической компоненты по отдельности. Наиболее интенсивно отражаются те его компоненты, для которых выполняется условие максимума интерференции, а наиболее слабо – для которых выполняется условие минимума. Таким образом, в отражённом свете плёнка окрашивается в составной оттенок, соответствующий, главным образом, тем длинам волн, для которых выполняется условие максимума интерференции отражённых волн при заданном угле падения. Монохроматические волны, для которых выполняется условие минимума интерференции, в составном оттенке совершенно не представлены. При повороте плёнки условие максимума будет выполняться уже для другого набора длин волн, следовательно, будет изменяться её оттенок.
При варьировании толщины плёнки в случае монохроматического света изменяется интенсивность её окраски. Если толщина плёнки переменна (например, она имеет форму клина), то при освещении монохроматическим светом в разных её местах образуются либо тёмные, либо светлые полосы – линии равной толщины. В случае клина эти линии (интерференционные полосы) параллельны ребру клина, они имеют одинаковую ширину и располагаются на одинаковом расстоянии друг от друга. Расстояние между интерференционными полосами ![]() зависит от угла схождения плоскостей, образующих клин, т.е. от максимальной толщины клина, если его ширина задана.
зависит от угла схождения плоскостей, образующих клин, т.е. от максимальной толщины клина, если его ширина задана.
При облучении белым светом полосы на клине становятся цветными, в каждой точке клина наибольший вклад в образующийся оттенок вносят те спектральные цвета, для которых в данной точке при данной толщине выполняется условие максимума. Если толщина клина в данном месте мала, то число волн, для которых одновременно выполняется условие максимума, также мало, у тонкого конца клина условие максимума может выполняться вообще только для одной длины волны. При большой толщине в одной и той же точке накладываются максимумы для большого числа длин волн, и тогда с увеличением толщины клина окраска постепенно приближается к белой.
Если освещать плоскопараллельную пластинку рассеянным светом, при котором угол падения света в разных местах пластинки будет различным, то возникнут интерференционные полосы другого вида – полосы равного наклона, каждая из которых является геометрическим местом точек, соответствующих одинаковому значению угла падения.
При наблюдении интерференции не в отражённом, а в проходящем через плёнку свете, в выражении для разности хода (1) будет отсутствовать слагаемое ![]() , обусловленное потерей полуволны при отражении света от верхней поверхности тонкой плёнки, т.е. разность хода интерферирующих волн будет иметь вид
, обусловленное потерей полуволны при отражении света от верхней поверхности тонкой плёнки, т.е. разность хода интерферирующих волн будет иметь вид
В этом случае при заданных значениях d, n и ![]() условие минимума сменится на условие максимума и наоборот. Таким образом, если для монохроматического света в отражённом свете плёнка выглядела максимально тёмной, то в проходящем свете она будет выглядеть максимально светлой и наоборот. В случае белого света для проходящего света плёнка окрасится в оттенок, дополнительный к тому, который она имела в отражённом свете при данных значениях d, n и
условие минимума сменится на условие максимума и наоборот. Таким образом, если для монохроматического света в отражённом свете плёнка выглядела максимально тёмной, то в проходящем свете она будет выглядеть максимально светлой и наоборот. В случае белого света для проходящего света плёнка окрасится в оттенок, дополнительный к тому, который она имела в отражённом свете при данных значениях d, n и ![]() . Это же касается и интерференции белого света на клине.
. Это же касается и интерференции белого света на клине.