 |
| Рис. 1 |
Поместим в цепь переменного тока резистор с сопротивлением R (рис. 1) и подадим на его концы переменное напряжение ![]() , где ω – циклическая частота колебаний. По закону Ома ток в цепи равен
, где ω – циклическая частота колебаний. По закону Ома ток в цепи равен
| (1) |
где ![]() – амплитуда тока.
– амплитуда тока.
Отсюда видно, что сдвига фаз между током I и напряжением U нет.
 |
| Рис. 2 |
Подключим теперь к цепи переменного тока конденсатор ёмкости С (рис. 2) и подадим на него то же переменное напряжение. Тогда заряд на обкладке конденсатора равен ![]() . Сила тока в цепи равна
. Сила тока в цепи равна
| (2) |
где
| (3) |
Таким образом, в этом случае ток на данном участке цепи изменяется по гармоническому закону с той же частотой, что и подаваемое напряжение, но опережает его по фазе на ![]() . Величина
. Величина ![]() имеет размерность сопротивления, и в формуле (3), связывающей амплитуды тока и напряжения, она играет как раз эту роль. Эта величина называется емкостным сопротивлением. В предельном случае нулевой частоты она стремится к бесконечности, это означает, что в цепи постоянного тока конденсатор является разрывом в цепи, и ток через него не протекает. При увеличении частоты переменного напряжения емкостное напряжение уменьшается, а для очень высоких частот оно становится ничтожно малым. Это означает, что при больших частотах ток через конденсатор может достигать больших величин. Конечно, электроны движутся только по подводящим к обкладкам конденсатора проводам, между обкладками никакого движения зарядов нет. Однако между обкладками конденсатора имеется быстропеременное электрическое поле, т.е. ток смещения, равный току проводимости в подводящих проводах.
имеет размерность сопротивления, и в формуле (3), связывающей амплитуды тока и напряжения, она играет как раз эту роль. Эта величина называется емкостным сопротивлением. В предельном случае нулевой частоты она стремится к бесконечности, это означает, что в цепи постоянного тока конденсатор является разрывом в цепи, и ток через него не протекает. При увеличении частоты переменного напряжения емкостное напряжение уменьшается, а для очень высоких частот оно становится ничтожно малым. Это означает, что при больших частотах ток через конденсатор может достигать больших величин. Конечно, электроны движутся только по подводящим к обкладкам конденсатора проводам, между обкладками никакого движения зарядов нет. Однако между обкладками конденсатора имеется быстропеременное электрическое поле, т.е. ток смещения, равный току проводимости в подводящих проводах.
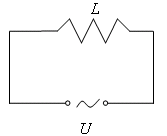 |
| Рис. 3 |
Теперь подключим катушку с индуктивностью L и пренебрежимо малым сопротивлением к цепи переменного тока с синусоидальным напряжением ![]() (рис. 3). Запишем закон Ома для участка цепи с ЭДС
(рис. 3). Запишем закон Ома для участка цепи с ЭДС ![]() . В нашем случае
. В нашем случае ![]() , а
, а ![]() – это ЭДС самоиндукции
– это ЭДС самоиндукции ![]() . Таким образом
. Таким образом ![]() , т.е.
, т.е. ![]() . Интегрируя это соотношение, получаем
. Интегрируя это соотношение, получаем
| (4) |
где
| (5) |
Из формулы (4) видно, что в этом случае ток изменяется по гармоническому закону с той же частотой, что и подаваемое напряжение, однако отстаёт от него по фазе на ![]() . Величина
. Величина ![]() , имеющая размерность сопротивления, называется индуктивным сопротивлением катушки. Из формулы (5) видно, что при больших частотах индуктивное сопротивление велико, следовательно, амплитуда тока мала. В случае постоянного тока индуктивное сопротивление, напротив, равно нулю.
, имеющая размерность сопротивления, называется индуктивным сопротивлением катушки. Из формулы (5) видно, что при больших частотах индуктивное сопротивление велико, следовательно, амплитуда тока мала. В случае постоянного тока индуктивное сопротивление, напротив, равно нулю.
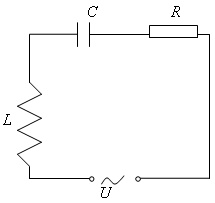 |
| Рис. 4 |
Рассмотрим теперь цепочку, состоящую из последовательно соединённых омического сопротивления R, катушки индуктивности L и конденсатора ёмкости С (рис. 4), подсоединенную к источнику переменного напряжения ![]() . В этом контуре пусть протекает переменный синусоидальный ток силой
. В этом контуре пусть протекает переменный синусоидальный ток силой ![]() . Таким образом мы сделали совершенно естественное предположение о том, что частота изменения тока такая же, как и частота изменения напряжения, но фазы тока и напряжения не совпадают.
. Таким образом мы сделали совершенно естественное предположение о том, что частота изменения тока такая же, как и частота изменения напряжения, но фазы тока и напряжения не совпадают.