Энергия взаимодействия отражает тенденцию системы к установлению в ней полного порядка, именно при полном порядке (в нашем случае при h = 1) энергия минимальна, что соответствовало бы устойчивому равновесию при отсутствии теплового движения. Энтропия системы, напротив, отражает тенденцию к максимальному молекулярному хаосу, к максимальному тепловому движению. Чем сильнее тепловое движение, тем больше энтропия, и если бы не было взаимодействия молекул друг с другом, то система стремилась бы к максимальному хаосу с максимальной энтропией.

В реальной же системе имеются обе эти тенденции, и это проявляется в том, что при постоянных объеме и температуре в состоянии термодинамического равновесия достигает экстре­мального (минимального) значения не энергия и не энтропия, а свободная энергия Гельмгольца:

F = U – T S.

Для нашего случая из формул (6) и (7) можно получить:

(8)

В состоянии термодинамического равновесия степень упорядочения должна быть такой, чтобы свободная энергия была бы минимальной, поэтому мы должны исследовать функцию (8) на экстремум, взяв от нее производную по h и приравняв ее к нулю. Таким образом, условие равновесия примет вид

(9)

В  этом уравнении – безразмерная температура.

Рис. 2

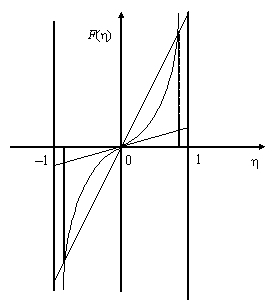
Уравнение (9) – трансцендентное, и его можно решить численными методами. Однако его решение можно исследовать графически. Для этого нужно построить графики функций, стоящих в левой и правой частях уравнения, при различных значениях параметра t. Обозначим эти функции соответственно F₁ и F₂
(рис. 2).

Функция F₁ не зависит от параметра t, она представляет собой кривую с двумя вертикальными асимптотами при  значениях переменной  h, равных  +1  и –1. Функция эта монотонно возрастает, она нечетная, ее производная в начале координат равна . Функция F₂ изображается прямой, проходящей через начало координат, ее наклон зависит от параметра t: чем меньше t, тем больше тангенс угла наклона, который равен  .

Если t > 1, то , тогда кривые пересекаются только в начале координат, т.е. в этом случае уравнение (9) имеет лишь одно решение h = 0. При t < 1 кривые пересекаются в трех точках, т.е. уравнение (9) имеет 3 решения. Одно из них по-прежнему нулевое, два других отличаются лишь знаком.

Оказывается, что нулевое решение при t < 1 соответствует не минимуму, а максимуму свободной энергии, и поэтому состоянию термодинамического равновесия соответствует  другое, т. е. ненулевое решение. При этом оба ненулевых решения описывают фактически одно и то же состояние, отличающиеся лишь заменой местами атомов А и В (т. е. моментов «вверх» и «вниз»).

Подставив значение t = 1, получим значение температуры, разделяющей два типа решений уравнения (9):

Эта температура называется температурой, или точкой Кюри для перехода ферромагнетик–парамагнетик, или просто критической температурой.

При более низких температурах магнетик существует в упорядоченном ферромагнитном состоянии, а при более высоких – дальний порядок в расположении магнитных моментов атомов отсутствует, и вещество является парамагнетиком. Отметим, что данный переход является фазовым переходом второго рода, параметр порядка h постепенно уменьшается с увеличением температуры и в критической точке становится равным нулю.

Зависимость параметра порядка h от приведенной температуры t, полученная из решения уравнения (9), показана на рис. 3.

Свободная энергия (8) для ферромагнетика во внешнем поле запишется:

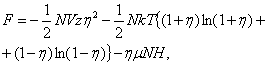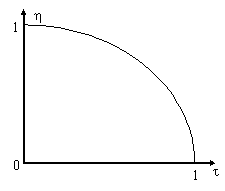Рис. 3

где m – магнитный момент атома. В этой формуле второе слагаемое представляет собой энергию взаимодействия магнитных моментов атомов с внешним магнитным полем, равную . Общий случай ферромагнетика в магнитном поле математически исследовать довольно трудно, ограничимся лишь рассмотрением ферромагнетика при температурах выше точки Кюри. Тогда  уравнение равновесия, аналогичное (9), примет вид:

Ограничимся случаем слабого намагничивания, которое наблю­дается при температурах значительно выше точки Кюри (Т ≫ T_C) и слабых магнитных полях. При h ≪ 1 левую часть этого уравнения можно разложить в ряд, ограничиваясь линейными членами, т. е.

ln (1+h) » h. Тогда 2kTh = mН +2hkТ_С, и намагниченность , т. е. парамагнитная восприимчивость. Таким образом, восприимчивость ферромагнетика при температурах выше точки Кюри в слабых магнитных полях обратно пропорциональна (Т – Т_С)_, т. е. наблюдается согласие теории с экспериментальным законом Кюри–Вейсса.