Электропроводность проводника определяется наличием в нем свободных носителей заряда (электроны в металле, электроны и дырки в полупроводнике, ионы разного знака в электролитах). Предположим здесь, что носители тока слабо взаимодействуют друг с другом, а взаимодействие их с ионами кристаллической решетки или с молекулами примеси сводится к соударениям. Кроме того, будем считать, что движение этих частиц подчиняется законам классической механики.

Рассмотрим движение одной такой частицы. Пусть заряженная частица с зарядом е и массой m движется в однородном электрическом поле. Сила, действующая на частицу со стороны поля, равна , где – напряженность поля. Тогда уравнение ее движения имеет вид

Пусть вектор напряженности направлен по оси Ох, тогда проекция скорости частицы на другие координатные оси остается постоянной во время движения, а проекция ее скорости на ось Ох изменяется со временем по закону: , где – проекция скорости частицы на ось Ох в начальный момент времени.

Вычислим среднее значение проекций скорости этой частицы за некоторое время , т.е., например, 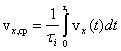. Тогда получим:

,

. (1)

В отсутствие электрического поля частицы в проводнике (которые приближенно можно считать свободными) совершают хаотическое тепловое движение, сталкиваясь при этом с ионами на узлах кристаллической решетки, с атомами примесей и т.д. Все направления движения свободных частиц равноправны, и какого-нибудь потока частиц, т.е. тока, не возникает. Поэтому усредненные по всему коллективу частиц проекции скорости (обозначим их  áv_xñ и áv_y ñ)  равны нулю.

Если проводник находится в электрическом поле, то на частицы действуют направленные силы. Если следить за какой-нибудь частицей, то можно обнаружить, что на тепловое хаотическое движение частицы накладывается направленное движение ее под действием силы со стороны электрического поля (так называемый дрейф). Если под в формуле (1) понимать промежуток времени между двумя какими-нибудь последовательными столкновениями частицы, то v_x,cp и v_y,cp есть средние значения проекции скорости этой частицы в течение данного промежутка времени _. Чтобы найти проекции скорости дрейфа частиц  áv_хñ и áv_уñ, необходимо еще раз усреднить выражение (1) по всем возможным промежуткам времени между последовательными столкновениями .

Под величинами v_x0 и v_y0 следует понимать значения проекций скорости частицы сразу же после какого-то столкновения. Ввиду хаотичности теплового движения можно считать, что их средние значения равны нулю. Усредняя уравнения (1) по всем временам столкновений (не забывая при этом, что константы можно выносить из-под знака усреднения), получаем:

, (2)

где áv_xñ и áv_yñ – средние значения проекций скорости направленного движения носителей тока; átñ –  среднее время между двумя последовательными столкновениями.

В данном случае вектор плотности тока направлен вдоль оси Ох. Величина j пропорциональна средней скорости направленного движения, а именно j = е n áv_xñ, где  n – число носителей тока в единице объема. Подставляя сюда áv_хñ из формулы (2), получим

. (3)

Это выражение называют законом Ома в дифференциальной форме. Величина

(4)

называется коэффициентом электропроводности или просто электропроводностью данного проводника, а коэффициент пропорциональности между средней скоростью направленного движения зарядов áv_xñ и напряженностью приложенного электрического поля Е называют подвижностью носителей тока. Из формулы (2) видно, что подвижность выражается следующим образом:

Электропроводность и подвижность связаны друг с другом соотношением:  s = e n l.

Закон Ома выполняется для металлов, полупроводников, электролитов, т.е. для тех веществ, в которых носители тока испытывают большое число соударений. При этом данный закон выполняется при не слишком сильных полях, когда роль соударений велика. Закон Ома не выполняется при токах в вакууме (например, в кинескопах, радиолампах, ускорителях частиц), так как в этих случаях носители тока практически не испытывают столкновений. Закон Ома очень ограниченно выполняется в плазме, так как в плазме обычно непостоянно число носителей тока.

Отметим, что выражение для коэффициента электропроводности (4) является гораздо более неточным, чем сам закон Ома. Это соотношение более или менее применимо для полупроводников или электролитов, но совершенно не пригодно для металлов, в то время как сам закон  Ома для металлов выполняется достаточно хорошо.