Вектором Шепли называется дележ , компоненты которого определяются формулой

.

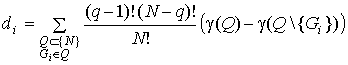(6.2)

Суммирование в (6.2) ведется по всем коалициям и по всем игрокам, входящим в эту коалицию. Величина , фигурирующая в (6.2), означает число игроков в коалиции .

Формуле (6.2) можно дать следующее истолкование. Пусть игроки решили встретиться в определенном месте. Очередность их прибытия на встречу случайна, но все порядки прибытия игроков (т.е. их перестановки) имеют одну и ту же вероятность . Предположим, что если игрок , прибывая, застает на месте членов коалиции , и только их, то он получает долю выигрыша в размере ; иначе говоря, его выигрышем является предельная величина, которую он вносит в коалицию. Тогда компонента вектора Шепли представляет собой математическое ожидание выигрыша игрока .