Применяется, когда известны вероятности   свершения состояний природы. Оптимальное решение  выбирается из условия максимума среднего выигрыша ЛПР при заданных вероятностях свершения состояний природы, т.е. из условия

.

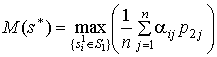(5.2)

      Пример 5.1. Фирма (ЛПР) может предложить к реализации один из трех видов продукции: . При этом рынок (природа) может иметь одно из трех возможных состояний . Прибыли от реализации каждого из товаров при любом состоянии рынка и заданы в матрице полезности:

      Оптимальное по критерию Лапласа решение находим из условия (5.1). Имеем:

;  ;

.

Поскольку , то в качестве оптимального решения с одинаковым успехом могут быть взяты решения  или , доставляющие одинаковое максимальное значение среднего выигрыша ЛПР.

      Для использования критерия ожидаемого значения нужно знать априорные вероятности свершения состояний природы. Пусть эти вероятности известны и равны . Оптимальное по критерию ожидаемого значения решение для заданных априорных вероятностях находим из условия (5.2). Имеем:

;  ;

.

Поскольку 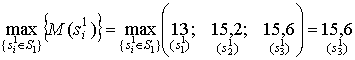, то оптимальным по критерию ожидаемого значения с заданными априорными вероятностями состояний природы решением следует взять  как доставляющие максимальное значение среднего выигрыша ЛПР.