Более глубокое изучение регрессионных моделей начнем с модели парной линейной регрессии. Эта модель является частным случаем модели многомерной регрессии, но ее изучение представляет самостоятельный интерес, поскольку она имеет многие характерные свойства общих многомерных моделей, но более наглядна и проста для изучения.

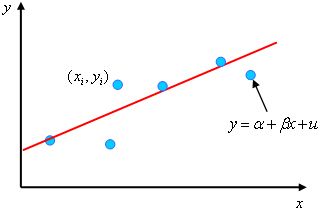
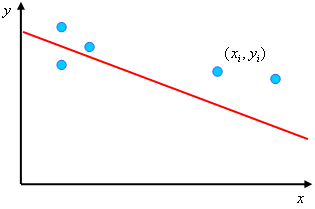
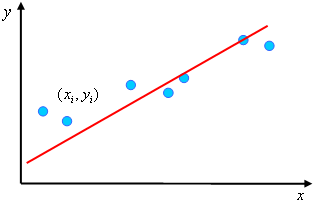
Парная линейная регрессионная модель используется для описания линейной функциональной взаимосвязи двух переменных, если исходя из анализа объекта исследования предполагается, что такая связь объективно существует. Вывод о предполагаемой линейной зависимости можно сделать, построив так называемую диаграмму рассеяния, на которой в плоскости графически отображаются точки с координатами , , соответствующие наблюдаемым значениям переменных. Примеры диаграмм рассеяния приведены на рис. 2.1,а, б, в. По виду этих диаграмм можно сделать предположение, что между переменными и возможно существует приближенная линейная зависимость.

Замечание. Следует иметь в виду, что предположение о наличии линейной связи основано лишь на ограниченном фиксированном числе наблюдений, которыми располагает аналитик. Возможно, что если бы наблюдений было больше, то это позволило сделать предположение о некоторой, отличной от линейной, закономерности.

а)	б)
в)

Рис. 2.1. Диаграммы рассеяния,
по виду которых можно предположить существование линейной зависимости