Пуассоновский поток событий является одним из самых «любимых» потоков в теории массового обслуживания. Он характеризуется выполнением двух свойств:

1.Отсутствие последствия.

2.Ординарность.

Прежде чем выводить формулы, введем обозначения и сделаем некоторые  следствия из ординарности. Пусть P_k (t₀ ,t), есть вероятность того, что на интервале [t₀; t] наступит ровно k событий. Тогда, в силу определения интенсивности, функция

                                      

(1)

будет интенсивностью пуассоновского потока. Это же соотношение можно записать так:

                                 

P1(t ,t +Δt) = λ(t)Δt +ο(Δt).

(2)

В силу ординарности потока

,  при  k ≥ 2,

и поэтому при k ≥ 2

                                      

Pk (t ,t +Δt) = ο(Δt).

(3)

Так как выполнено условие нормировки

P₀ (t ,t +Δt) + P₁ (t ,t +Δt) + P_>1 (t ,t +Δt) = 1,

то

     

P0 (t ,t +Δt) = 1– P1 (t ,t +Δt) – P>1 (t ,t +Δt) = 1– λ(t)Δt +ο(Δt).

(4)

Соотношения (2) – (4) являются основными для дальнейшего.

Выведем систему дифференциальных уравнений, определяющую P_k (t₀ ,t). Учитывая отсутствие последствия, можно записать:

P₀ (t ₀,t +Δt) = P₀ (t₀ ,t) P₀ (t ,t +Δt) = P₀ (t₀ ,t)[ 1– λ(t)Δt +ο(Δt)],

отсюда

.

Переходя к пределу Δt → 0, получим

Аналогично для P_k (t₀ ,t) можно записать:

Используя соотношения (2) – (4), запишем

P_k (t ₀,t +Δt) = P_k (t₀ ,t) [1– λ(t)Δt +ο(Δt)] + P_k-1 (t₀ ,t) [λ(t)Δt +ο(Δt)] + ο(Δt),

откуда

и после предельного перехода Δt → 0 получим

.

Итак,

                  

,   k ≥ 1.

(5)

Для однозначного решения этой системы надо добавить граничное условие, которое естественно брать в виде

                                  

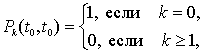(6)

так как в силу ординарности потока на интервале нулевой длины с вероятностью 1 не будет ни одного события.

Рассмотрим решение системы (5) методом производящих функций. Введем функцию

.

Умножая первое уравнение системы (5) на z⁰, а все остальные – на соответствующие z^k и суммируя все равенства, получим

Поэтому окончательно

                         

.

(7)

Это уравнение легко решается методом разделения переменных

,

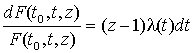откуда, интегрируя в пределах (t₀, t), получим

.

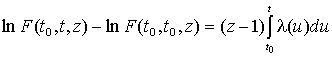Но, как следует из граничного условия (6),

F(t₀ ,t₀ ,z) = 1,

и поэтому

,

где

.

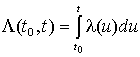Разлагая  в ряд Тейлора, запишем

,

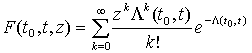откуда получаем основную формулу, относящуюся к пуассоновскому потоку:

                                  

.

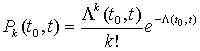(8)

Эта формула, вместе с формулами (2 – 4) и позволяет решать практически все задачи, относящиеся к пуассоновскому потоку.