Логические величины принимают только два значения – TRUE (истина) и FALSE (ложь). К ним можно применять логические операции, основными из которых являются: AND (конъюнкция – логическое И), OR (дизъюнкция – логическое ИЛИ) и NOT (инверсия – логическое отрицание).
В некоторых программах конъюнкция обозначается знаками & или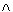 
, например
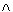B.В некоторых программах дизъюнкция обозначается знаками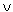 
или |, например
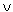B или A | B.В некоторых программах конъюнкция обозначается знаками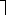 
(или ¯ ), например
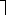A или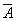 
.Первые две операции применяются к двум логическим величинам (например, a AND b или c OR d), а операция NOT – к одной (например, NOT a). Результатом выражения с логическими данными (логические выражения) является логическая величина. Результат операции AND равен TRUE только в том случае, если обе величины равны TRUE, в остальных случаях результат равен FALSE. Если применяется операция OR, то результат равен FALSE только в том случае, если обе величины FALSE, в остальных случаях результат равен TRUE. Операция NOT изменяет значение логической величины: результат равен TRUE, если величина равна FALSE, и наоборот. Среди логических первой выполняется операция Not, затем And и последней Or. Порядок выполнения операций может быть изменен использованием скобок.
Например, если
то выражение
равно TRUE
При этом используются следующие обозначения
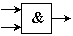или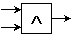 
– конъюнкция;
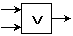или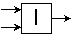 
– дизъюнкция;
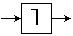или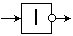 
– инверсия.
Можно для обозначения одной вершиной сразу двух операций «И–НЕ», «ИЛИ–НЕ» использовать следующую форму:
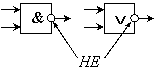
Это позволяет сократить схему. Конструкцию «ИЛИ–НЕ» еще называют логической операцией «исключающее ИЛИ» и для ее обозначения используют следующий элемент схемы:
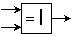
Например, логическое выражение
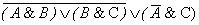
может быть представлено схемой
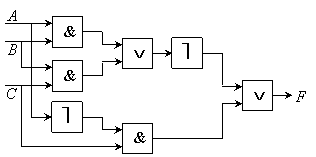
Например, схема
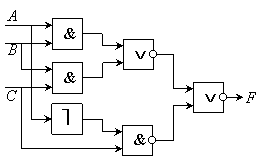
представляет логическое выражение
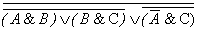.В смешанных выражениях операции выполняются в соответствии с приоритетами. При этом наивысший приоритет у арифметических операций, затем выполняются операции сравнения и самый низкий приоритет у логических операций. Операции с одинаковым приоритетом выполняются слева направо.
Для упрощения логических выражений можно использовать следующие соотношения:
1. 
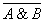эквивалентно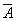 
;
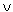
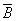2. 
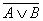эквивалентно & ;
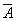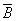3. A 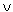A & B = A & (1 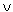B) = A.
В их справедливости можно убедиться, проверив результаты логических выражений при всех возможных значениях A и B. Первое и второе соотношения носят названия законов Моргáна.
Например, в результате упрощения логического выражения F =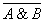 
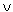
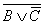
получится выражение
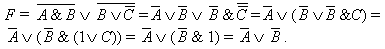
Для упрощения логических выражений можно использовать различные соотношения. Для представления логических выражений часто используется так называемая логическая схема. В такой схеме вершины соответствуют логическим операциям, а дуги показывают, к каким именно логическим величинам применяются эти операции.